题目内容
某校数学课外小组,在坐标纸上为学校的一块空地设计植树方案如下:
第K棵树种植在Pk(Xk,Yk)处,其中X1=1,Y1=1,当k≥2时,Xk=Xk-1+1-5([
]-[
]),Yk=Yk-1+[
]-[
],[a]表示非负实数a的整数部分,例如[2.6]=2,[0.2]=0,按此方案,第2013棵树种植点的坐标是( )
第K棵树种植在Pk(Xk,Yk)处,其中X1=1,Y1=1,当k≥2时,Xk=Xk-1+1-5([
| k-1 |
| 5 |
| k-2 |
| 5 |
| k-1 |
| 5 |
| k-2 |
| 5 |
| A、(3,402) |
| B、(3,403) |
| C、(4,403) |
| D、(5,403) |
考点:坐标确定位置
专题:规律型
分析:由题意可知,数列xn为1,2,3,4,5,1,2,3,4,5,1,2,3,4,5,…;数列{yn}为1,1,1,1,1,2,2,2,2,2,3,3,3,3,3,4,4,4,4,4,…由此入手能够得到第6棵树种植点的坐标和第2013棵树种植点的坐标.
解答:解:∵T(
)-T(
)组成的数列为0,0,0,0,1,0,0,0,0,1,0,0,0,0,1…,k=2,3,4,5,…
一一代入计算得数列xn为1,2,3,4,5,1,2,3,4,5,1,2,3,4,5,…
即xn的重复规律是x5n+1=1,x5n+2=2,x5n+3=3,x5n+4=4,x5n=5.n∈N*.
数列{yn}为1,1,1,1,1,2,2,2,2,2,3,3,3,3,3,4,4,4,4,4,…
即yn的重复规律是y5n+k=n,0≤k<5.
∴由题意可知第6棵树种植点的坐标应为(1,2);第2013棵树种植点的坐标应为(3,403).
故选B.
| k-1 |
| 5 |
| k-2 |
| 5 |
一一代入计算得数列xn为1,2,3,4,5,1,2,3,4,5,1,2,3,4,5,…
即xn的重复规律是x5n+1=1,x5n+2=2,x5n+3=3,x5n+4=4,x5n=5.n∈N*.
数列{yn}为1,1,1,1,1,2,2,2,2,2,3,3,3,3,3,4,4,4,4,4,…
即yn的重复规律是y5n+k=n,0≤k<5.
∴由题意可知第6棵树种植点的坐标应为(1,2);第2013棵树种植点的坐标应为(3,403).
故选B.
点评:本题考查数列的性质和应用,解题时要注意创新题的灵活运用.

练习册系列答案
 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
如果数轴上表示a、b两个数的点都在原点的左侧,且a在b的左侧,则|a-b|+
的值为( )
| (a+b)2 |
| A、-2b | B、2b |
| C、2a | D、-2a |
 观察函数y1和y2的图象,当x=0,两个函数值的大小为( )
观察函数y1和y2的图象,当x=0,两个函数值的大小为( )| A、y1>y2 |
| B、y1<y2 |
| C、y1=y2 |
| D、y1≥y2 |
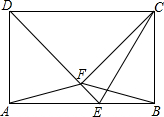 如图,E为矩形ABCD边AB上一点,AB=14,CE=13,DE=15,CF⊥DE于点F,连结AF、BF.则△ABF的面积为
如图,E为矩形ABCD边AB上一点,AB=14,CE=13,DE=15,CF⊥DE于点F,连结AF、BF.则△ABF的面积为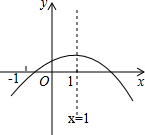 已知二次函数图象y=ax2+bx+c(a≠0)的图象如图,有下列4个结论.
已知二次函数图象y=ax2+bx+c(a≠0)的图象如图,有下列4个结论.
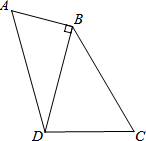 如图,在四边形ABCD中,AB=2,∠A=∠C=60°,DB⊥AB于点B,∠DBC=45°,求BC的长.
如图,在四边形ABCD中,AB=2,∠A=∠C=60°,DB⊥AB于点B,∠DBC=45°,求BC的长.