题目内容
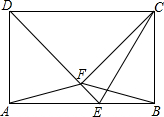 如图,E为矩形ABCD边AB上一点,AB=14,CE=13,DE=15,CF⊥DE于点F,连结AF、BF.则△ABF的面积为
如图,E为矩形ABCD边AB上一点,AB=14,CE=13,DE=15,CF⊥DE于点F,连结AF、BF.则△ABF的面积为考点:矩形的性质
专题:
分析:设AE=x,表示出BE=14-x,然后利用勾股定理列式求出x,从而得到矩形的宽AD,利用三角形的面积列式求出CF,再过点F作FG⊥CD于G,然后利用∠DCF的正弦列式求出FG,再求出点F到AB的距离,然后根据三角形的面积公式列式计算即可得解.
解答: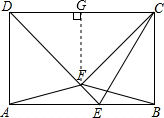 解:设AE=x,则BE=14-x,
解:设AE=x,则BE=14-x,
由勾股定理得,AD2=DE2-AE2=225-x2,
BC2=CE2-BE2=169-(14-x)2,
∵AD=BC,
∴225-x2=169-(14-x)2,
解得x=9,
∴AD=
=12,
∵CF⊥DE,
∴S△CDE=
×15•CF=
×14×12,
解得CF=
,
在Rt△CDF中,DF=
=
=
,
过点F作FG⊥CD于G,
则sin∠DCF=
=
,
即
=
,
解得GF=
,
∴点F到AB的距离=12-
=
,
△ABF的面积=
×14×
=36.96.
故答案为:36.96.
 解:设AE=x,则BE=14-x,
解:设AE=x,则BE=14-x,由勾股定理得,AD2=DE2-AE2=225-x2,
BC2=CE2-BE2=169-(14-x)2,
∵AD=BC,
∴225-x2=169-(14-x)2,
解得x=9,
∴AD=
| 225-81 |
∵CF⊥DE,
∴S△CDE=
| 1 |
| 2 |
| 1 |
| 2 |
解得CF=
| 56 |
| 5 |
在Rt△CDF中,DF=
| CD2-CF2 |
142-(
|
| 42 |
| 5 |
过点F作FG⊥CD于G,
则sin∠DCF=
| GF |
| CF |
| DF |
| CD |
即
| GF | ||
|
| ||
| 14 |
解得GF=
| 168 |
| 25 |
∴点F到AB的距离=12-
| 168 |
| 25 |
| 132 |
| 25 |
△ABF的面积=
| 1 |
| 2 |
| 132 |
| 25 |
故答案为:36.96.
点评:本题考查了矩形的性质,三角形的面积,勾股定理,锐角三角函数,综合题,但难点不大,利用勾股定理列出方程,然后求出矩形的宽是解题的关键,难点在于求出点F到AB的距离.

练习册系列答案
相关题目
在函数y=
的图象上,有三个点(1,y1),(
,y2),(-3,y3),则y1,y2,y3的大小关系为( )
| 1 |
| x |
| 1 |
| 2 |
| A、y1<y2<y3 |
| B、y3<y2<y1 |
| C、y2<y1<y3 |
| D、y3<y1<y2 |
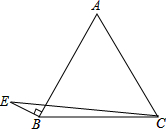 如图,已知:等边△ABC,AB=2
如图,已知:等边△ABC,AB=2 如图的运算程序中,若开始输入的x值为48,则第1次输出的结果为24,第2次输出的结果为12,…,第2014次输出的结果为
如图的运算程序中,若开始输入的x值为48,则第1次输出的结果为24,第2次输出的结果为12,…,第2014次输出的结果为