题目内容
1.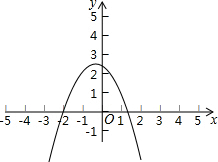 二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论:①abc>0;②a>b;③a-b+c>0;④4ac-8a>b2,其中正确的是①③(填序号)
二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论:①abc>0;②a>b;③a-b+c>0;④4ac-8a>b2,其中正确的是①③(填序号)
分析 由开口向下能得出a<0,抛物线与y轴交点在y轴正半轴可知c>0,对称轴-1<-$\frac{b}{2a}$<0可知0>b>2a,从而能得出①成立②不成立;当x=-1时,函数图象在x轴上方可得知a-b+c>0,即③成立;表示出抛物线的顶点坐标,由顶点的纵坐标>2,可得出4ac-8a<b2,即④不成立.结合上面结论即可得出只有①③成立.
解答 解:∵抛物线的开口朝下,
∴a<0;
∵抛物线与y轴交点在y的正半轴,
∴c>0;
∵抛物线的对称轴x=-$\frac{b}{2a}$在-1到0之间,即-1<-$\frac{b}{2a}$<0,
∴0>b>2a,即②不成立;
∵c>0,0>b>a,
∴abc>0,即①成立;
∵当x=-1时,抛物线上的点在x轴上方,
∴有a-b+c>0,即③成立;
由图可知,抛物线顶点(-$\frac{b}{2a}$,$\frac{4ac-{b}^{2}}{4a}$)的纵坐标大于2,
∴$\frac{4ac-{b}^{2}}{4a}$>2,
∵a<0,
∴4ac-b2<8a,
∴4ac-8a<b2,④不成立.
故答案为:①③.
点评 本题考查了二次函数图象与系数的关系,解题的关键是结合图象逐条分析.本题属于基础题,难度不大,解决该题型题目时,结合图象上的点找出二次函数各系数间的关系是关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
11.某市的中考各科试卷总分为600分,其中数学为120分,若用扇形统计图画出各科分数比例,则数学所占扇形圆心角为( )度.
| A. | 90 | B. | 45 | C. | 120 | D. | 72 |
12.为了鼓励市民节约用电,某市对居民用电实行“阶梯收费”(总电费=第一阶梯电费+第二阶梯电费).规定:用电量不超过200度按第一阶梯电价收费,超过200度的部分按第二阶梯电价收费.如图是张磊家2015年9月和10月所交电费的收据,则该市规定的第一阶梯电价和第二阶梯电价分别为每度( )
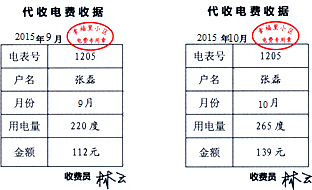

| A. | 0.5元、0.6元 | B. | 0.4元、0.5元 | C. | 0.3元、0.4元 | D. | 0.6元、0.7元 |
9.已知一次函数y=2x+2与x轴y轴分别交于A、B两点,另一直线y=kx+3交x轴正半轴于E、交y轴于F点,如△AOB与E、F、O三点组成的三角形相似,那么k值为( )
| A. | -0.5 | B. | -2 | C. | -0.5或-2 | D. | 以上都不对 |
16.在正三角形、平行四边形、矩形、菱形和圆这五个图形中,既是轴对称图形又是中心对称图形有( )
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
6.国务院总理作2009年政府工作报告时表示,今后三年各级政府拟投入医疗卫生领域的资金将达到850000000000元人民币,将数字850000000000用科学记数法表示为( )
| A. | 8.5×109 | B. | 8.5×1010 | C. | 8.5×1011 | D. | 8.5×1012 |
13.下列各数:①-12;②-(-1)2;③-13;④-(-1)-2,其中结果等于-1的是( )
| A. | ①②③ | B. | ①②④ | C. | ②③④ | D. | ①②③④ |
11.下列运算正确的是( )
| A. | (a+b)2=a2+b2 | B. | $\sqrt{a^2+b^2}$=$\sqrt{a^2}$+$\sqrt{b^2}$ | C. | a2•a3=a5 | D. | $\sqrt{{a}^{4}}$=±a2 |