题目内容
如果α是锐角，且cosα=
，求sinα，tanα的值．
解：∵cosα=，
∴sinα=
=
，
tanα=
=2
．
分析：根据同角的三角函数关系式：sin2α+cos2α=1，tanα=，进行计算．
点评：熟练运用同角的同角三角函数关系式进行求解．
，∴sinα=
=，tanα=
=2．分析：根据同角的三角函数关系式：sin2α+cos2α=1，tanα=
，进行计算．点评：熟练运用同角的同角三角函数关系式进行求解．
练习册系列答案
全能测控一本好卷系列答案
相关题目
如果α是锐角，且cosα=
，那么sinα的值是（ ）
| 4 |
| 5 |
A、
| ||
B、
| ||
C、
| ||
D、2
|
如果α是锐角，且cosα=
，那么cos（90°-α）的值是（ ）
| 4 |
| 5 |
A、
| ||
B、
| ||
C、
| ||
D、
|
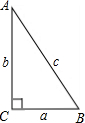我们知道，如果两个锐角的和等于一直角，那么这两个角互为余角，简称互余．如图，∠A与∠B互余，且有：sinA=