题目内容
14. 如图,∠A=30°,∠B=45°,∠C=40°,则∠DFE=( )
如图,∠A=30°,∠B=45°,∠C=40°,则∠DFE=( )| A. | 75° | B. | 100° | C. | 115° | D. | 120° |
分析 在△AEC中由三角形外角的性质可求得∠BEF,在△BEF中,利用三角形外角的性质可求得∠DFE.
解答 解:
∵∠BEF是△AEC的一个外角,
∴∠BEF=∠A+∠C=30°+40°=70°,
∵∠DFE是△BEF的一个外角,
∴∠DFE=∠B+∠BEF=70°+45°=115°,
故选C.
点评 本题主要考查三角形外角的性质,掌握三角形的一个外角等于不相邻两个内角的和是解题的关键.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
4. 图中所示的阴影部分为哪一个不等式的解集( )
图中所示的阴影部分为哪一个不等式的解集( )
 图中所示的阴影部分为哪一个不等式的解集( )
图中所示的阴影部分为哪一个不等式的解集( )| A. | x-y≤-5 | B. | x+y≥-5 | C. | x+y≤5 | D. | x-y≤5 |
5.下列说法正确的是( )
| A. | 经过一点有且只有一条直线 | B. | 射线OA=3cm | ||
| C. | 所有连接两点的线中,线段最短 | D. | 延长线段AB到C使AC=BC |
2.下列几何体从正面看、从左面看、从上面看完全相同的是( )
| A. |  圆锥 | B. |  长方体 | C. |  圆柱 | D. |  正方体 |
19.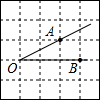 如图,在边长为1的小正方形组成的网格中,点A、B、O为格点,则tan∠AOB=( )
如图,在边长为1的小正方形组成的网格中,点A、B、O为格点,则tan∠AOB=( )
 如图,在边长为1的小正方形组成的网格中,点A、B、O为格点,则tan∠AOB=( )
如图,在边长为1的小正方形组成的网格中,点A、B、O为格点,则tan∠AOB=( )| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{3}$ | C. | $\frac{\sqrt{10}}{5}$ | D. | $\frac{\sqrt{5}}{3}$ |
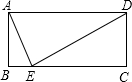 如图,已知在长方形ABCD中,点E在BC上,连接AE,DE,若AD=DE=14,∠BAE=15°,则CD的长为7.
如图,已知在长方形ABCD中,点E在BC上,连接AE,DE,若AD=DE=14,∠BAE=15°,则CD的长为7. 如图,已知抛物线y=ax2+bx+c(a≠0)与x轴交于点A(-4,0),B(1,0),与y轴交于点D(0,4),点C(-2,n)也在此抛物线上.
如图,已知抛物线y=ax2+bx+c(a≠0)与x轴交于点A(-4,0),B(1,0),与y轴交于点D(0,4),点C(-2,n)也在此抛物线上.