题目内容
16. 如图,AC⊥BC,垂足为C,BC=4,AC=3,⊙O与直线AC、BC、AB相切于点D、E、F,求⊙O的半径.
如图,AC⊥BC,垂足为C,BC=4,AC=3,⊙O与直线AC、BC、AB相切于点D、E、F,求⊙O的半径.
分析 根据AC、BA、BC与⊙O相切于点D、F、E;由勾股定理可得:BF=BE,AF=AD,CD=CE;可用DC分别表示出BE、BF的长,根据BF=BE,得出CD的表达式;连接OD、OE;易证得四边形ODCE是正方形,即OE=OD=CD,由此可求出⊙O的半径.
解答  解:∵AC⊥BC,
解:∵AC⊥BC,
∴∠ACB=90°,
∵BC=4,AC=3,
∴AB=5,
连接OD、OE;
∵AC、BE是⊙O的切线,
∴∠ODC=∠OEC=∠DCE=90°;
∴四边形ODCE是矩形;
∵OD=OE,
∴矩形ODCE是正方形;
即OE=OD=CD;
设CD=CE=x,则AD=AF=3-x;
连接OB,OF,
由勾股定理得:BF2=OB2-OF2,BE2=OB2-OE2,
∵OB=OB,OF=OE,
∴BF=BE,
则BA+AF=BC+CE,5+3-x=4+x,即x=2;
故⊙O的半径为2.
点评 本题考查了切线的性质,勾股定理,正方形的判定和性质,正确的作出辅助线是解题的关键.

练习册系列答案
相关题目
8.“十•一”黄金周期间,厦门鼓浪屿在7填中接待旅游的人数变化如下表(正数表示比前一天多的人数,负数表示比前一天少的人数)
若9月30日接待旅游人数记为a,
(1)请用a的代数式表示10月2日接待旅游的人数.
(2)若10月7日接待旅游人数为1.8万人,问9月30日接待旅游人数是多少万人?
| 日期 | 10月1日 | 10月2日 | 10月3日 | 10月4日 | 10月5日 | 10月6日 | 10月7日 |
| 人数变化 单位:万人 | +1.6 | +0.8 | -0.3 | -0.45 | 0.6 | +0.2 | -1.2 |
(1)请用a的代数式表示10月2日接待旅游的人数.
(2)若10月7日接待旅游人数为1.8万人,问9月30日接待旅游人数是多少万人?
5.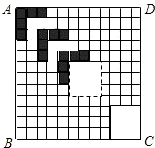 如图,正方形ABCD的边长为12,划分成12×12个小正方形格.将边长为n(n为整数,且2≤n≤11)的黑白两色正方形纸片按图中的方式黑白相间地摆放,第一张n×n的纸片正好盖住正方形ABCD左上角的n×n个小正方形格,第二张纸片盖住第一张纸片的部分恰好为(n-1)×(n-1)的正方形.如此摆放下去,最后直到纸片盖住正方形ABCD的右下角为止.
如图,正方形ABCD的边长为12,划分成12×12个小正方形格.将边长为n(n为整数,且2≤n≤11)的黑白两色正方形纸片按图中的方式黑白相间地摆放,第一张n×n的纸片正好盖住正方形ABCD左上角的n×n个小正方形格,第二张纸片盖住第一张纸片的部分恰好为(n-1)×(n-1)的正方形.如此摆放下去,最后直到纸片盖住正方形ABCD的右下角为止.
请你认真观察思考后回答下列问题:
(1)由于正方形纸片边长n的取值不同,完成摆放时所使用正方形纸片的张数也不同,请填写下表:
(2)设正方形ABCD被纸片盖住的面积(重合部分只计一次)为S1,未被盖住的面积为S2.
①当n=2时,求S1:S2的值;
②用含n的代数式表示S2.
 如图,正方形ABCD的边长为12,划分成12×12个小正方形格.将边长为n(n为整数,且2≤n≤11)的黑白两色正方形纸片按图中的方式黑白相间地摆放,第一张n×n的纸片正好盖住正方形ABCD左上角的n×n个小正方形格,第二张纸片盖住第一张纸片的部分恰好为(n-1)×(n-1)的正方形.如此摆放下去,最后直到纸片盖住正方形ABCD的右下角为止.
如图,正方形ABCD的边长为12,划分成12×12个小正方形格.将边长为n(n为整数,且2≤n≤11)的黑白两色正方形纸片按图中的方式黑白相间地摆放,第一张n×n的纸片正好盖住正方形ABCD左上角的n×n个小正方形格,第二张纸片盖住第一张纸片的部分恰好为(n-1)×(n-1)的正方形.如此摆放下去,最后直到纸片盖住正方形ABCD的右下角为止.请你认真观察思考后回答下列问题:
(1)由于正方形纸片边长n的取值不同,完成摆放时所使用正方形纸片的张数也不同,请填写下表:
| 纸片的边长n | 2 | 3 | 4 | 5 | 6 |
| 使用的纸片张数 | 11 | 10 | 9 | 8 | 7 |
①当n=2时,求S1:S2的值;
②用含n的代数式表示S2.
6. 有理数a、b在数轴上的位置如图所示,下列结论中正确的是( )
有理数a、b在数轴上的位置如图所示,下列结论中正确的是( )
 有理数a、b在数轴上的位置如图所示,下列结论中正确的是( )
有理数a、b在数轴上的位置如图所示,下列结论中正确的是( )| A. | a<b | B. | ab>0 | C. | a+b<0 | D. | a-b<0 |
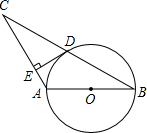 如图,△ABC中,AB=AC,且AB为⊙O的直径,⊙O交BC于点D,过D点作DE⊥AC于E
如图,△ABC中,AB=AC,且AB为⊙O的直径,⊙O交BC于点D,过D点作DE⊥AC于E