题目内容
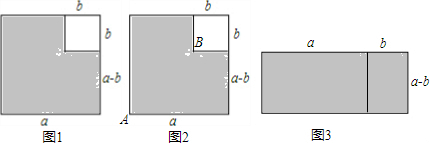
11.将一块直角三角板DEF放置在锐角△ABC上,使得该三角板的两条直角边DE、DF恰好分别经过点B、C.
(1)如图①,若∠A=40°时,点D在△ABC内,则∠ABC+∠ACB=140度,∠DBC+∠DCB=90度,∠ABD+∠ACD=50度;
(2)如图②,改变直角三角板DEF的位置,使点D在△ABC内,请探究∠ABD+∠ACD与∠A之间存在怎样的数量关系,并验证你的结论.
(3)如图③,改变直角三角板DEF的位置,使点D在△ABC外,且在AB边的左侧,直接写出∠ABD、∠ACD、∠A三者之间存在的数量关系.
分析 (1)根据三角形内角和定理可得∠ABC+∠ACB=180°-∠A=140°,∠DBC+∠DCB=180°-∠DBC=90°,进而可求出∠ABD+∠ACD的度数;
(2)根据三角形内角和定义有90°+(∠ABD+∠ACD)+∠A=180°,则∠ABD+∠ACD=90°-∠A.
(3)由(1)(2)的解题思路可得:∠ACD-∠ABD=90°-∠A.
解答 解:(1)在△ABC中,∵∠A=40°,
∴∠ABC+∠ACB=180°-40°=140°,
在△DBC中,∵∠BDC=90°,
∴∠DBC+∠DCB=180°-90°=90°,
∴∠ABD+∠ACD=140°-90°=50°;
故答案为:140;90;50.
(2)∠ABD+∠ACD与∠A之间的数量关系为:∠ABD+∠ACD=90°-∠A.证明如下:
在△ABC中,∠ABC+∠ACB=180°-∠A.
在△DBC中,∠DBC+∠DCB=90°.
∴∠ABC+∠ACB-(∠DBC+∠DCB)=180°-∠A-90°.
∴∠ABD+∠ACD=90°-∠A.
(3)∠ACD-∠ABD=90°-∠A.
点评 本题考查三角形外角的性质及三角形的内角和定理,实际上证明了三角形的外角和是360°,解答的关键是沟通外角和内角的关系.

练习册系列答案
相关题目
16.若一个多边形的内角和与它的外角和相等,则这个多边形是( )
| A. | 三角形 | B. | 四边形 | C. | 五边形 | D. | 六边形 |
3.下列调查中,适合用普查方式的是( )
| A. | 了解一批电视机的使用寿命 | B. | 了解全国六年级学生的视力情况 | ||
| C. | 了解渤海湾中鱼的种类 | D. | 了解你们班上的同学每周上网情况 |
20.下列运算中,正确的是( )
| A. | a3•a2=a5 | B. | a8÷a4=a2 | C. | (a3)2=a5 | D. | -(2a)2=4a2 |
1.下列运算中正确的是( )
| A. | (a3)2=a5 | B. | a2+a3=a5 | C. | (a+1)2=a2+1 | D. | a5÷a3=a2 |