��Ŀ����
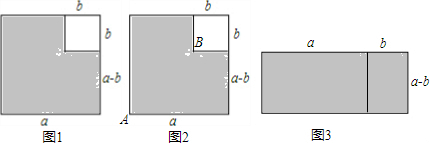
19����1������ͼ1���ӱ߳�Ϊa��������ֽƬ�м�ȥһ���߳�Ϊb��С�����Σ���ͼ1�е���Ӱ�������Ϊs����s=a2-b2���ú�a��b����ʽ��ʾ��������ͼ1�е�ͼ�Σ������߶�AB��������ͼ2�����Ѽ��ɵ�����ֽƬƴ����ͼ3�ij����Σ���д�����������������ֵij˷���ʽ��
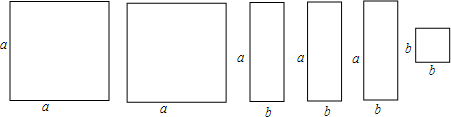
��2������ֽƬ���������DZ߳�Ϊa�������Σ������dz�Ϊa����Ϊb�ij�����ֽƬ��һ���DZ߳�Ϊb��������ֽƬ�����ܷ���ЩֽƬƴ��һ�������Σ����㻭����ͼ����д����Ӧ�ĵ�ʽ��
���� ��1�������������ε������ʽ����Ӱ���ֵ����=�������ε����-�հײ���С�����ε������
�����ó����ε������ʽ��ͼ3�����������е���Ӱ���������ʽ���ɣ�
��2��ƴ�ɳ����εij�Ϊb+2a����Ϊa+b�����㳤���ε�������ɵõ����ۣ�
���  �⣺��1������Ӱ���ֵ����s=a2-b2��
�⣺��1������Ӱ���ֵ����s=a2-b2��
�ʴ�Ϊ��a2-b2��
�ڡ�ͼ3��s=��a+b����a-b����
��a2-b2=��a+b����a-b����
��2��ƴ�ӵij�������ͼ��ʾ��
��Ϊ��b+2a������Ϊa+b�����Ϊb2+3ab+2a2��
���ԣ��õ��ĵ�ʽΪ��b+2a����a+b��=b2+3ab+2a2��
���� ������Ҫ�������ƽ���ʽ�ļ��α�ʾ�����ò�ͬ������ʾ����ǽ���Ĺؼ���

��ϰ��ϵ�д�
�����Ŀ
9���ҹ�������ȫ���˿��ղ�������ʾ����ס�ڳ�����˿�������ԼΪ6 6600 0000�ˣ��ÿ�ѧ��������ʾΪ��������
| A�� | 66.6��107 | B�� | 6.66��108 | C�� | 6.66��107 | D�� | 0.666��109 |
4����һ�������Ĵ�����װ�к졢��������ɫ����20����ÿ�������ɫ����ȫ��ͬ��ijѧϰ��ȤС��������ʵ�飬������Ⱥ�����������1��������ɫ���ٷŻش��У������ظ����±��ǻ�����еIJ���ͳ�����ݣ�
��1������ϱ���
��2�����������ĸ��ʵĹ���ֵ��0.6����ȷ��0.1��
��3���Թ�������к���ĸ�����
| ����Ĵ���n | 100 | 150 | 200 | 500 | 800 | 1000 |
| ��������Ĵ���m | 59 | 96 | 118 | 290 | 480 | 601 |
| ���������Ƶ��$\frac{m}{n}$ | 0.59 | 0.64 | 0.58 | 0.58 | 0.60 | 0.601 |
��2�����������ĸ��ʵĹ���ֵ��0.6����ȷ��0.1��
��3���Թ�������к���ĸ�����
8������˵����ȷ���ǣ�������
| A�� | ��ȵĽ��ǶԶ��� | |
| B�� | ��ͬһƽ���ڣ���a�Ab��b�Ac����a��c | |
| C�� | �ڴ������ | |
| D�� | ��һ������ֻ��һ��ֱ������ֱ֪��ƽ�� |





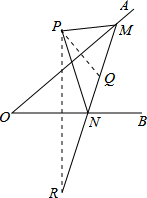 ��ͼ����P�ǡ�AOB��һ�㣬��M��N�ֱ��ǡ�AOB�����ϵĵ㣬��P����OA�ĶԳƵ�Qǡ�������߶�MN�ϣ���P����OB�ĶԳƵ�R�����߶�MN���ӳ����ϣ���PM=2.5cm��PN=3cm��MN=4cm�����߶�QR�ij�Ϊ4.5cm��
��ͼ����P�ǡ�AOB��һ�㣬��M��N�ֱ��ǡ�AOB�����ϵĵ㣬��P����OA�ĶԳƵ�Qǡ�������߶�MN�ϣ���P����OB�ĶԳƵ�R�����߶�MN���ӳ����ϣ���PM=2.5cm��PN=3cm��MN=4cm�����߶�QR�ij�Ϊ4.5cm��