题目内容
已知点P是边长为4的正方形ABCD的AD边上一点，AP=1，BE⊥PC于E，则BE=分析：在Rt△PDC中，由勾股定理可求出PC的长，由于四边形ABCD是正方形且BE⊥PC于E，可证出△BEC∽△CDP，所以
=
，分别将BC、CD、PC的值代入即可求出BE的长．
| BE |
| CD |
| BC |
| PC |
解答：
解：如下图所示：PD=AD-AP=4-1=3
在Rt△PDC中，PD=AD-AP=4-1=3，DC=4，
由勾股定理可得：PC2=PD2+DC2，
即：PC=
=
=5，
∵∠BCE+∠CBE=90°，∠BCE+∠DCP=90°
∴∠CBE=∠DCP，
又∵∠BEC=∠D=90°，
∴△BEC∽△CDP，
∴
=
，
∴BE=
×CD=
×4=
．
解：如下图所示：PD=AD-AP=4-1=3在Rt△PDC中，PD=AD-AP=4-1=3，DC=4，
由勾股定理可得：PC2=PD2+DC2，
即：PC=
| PD2+DC2 |
| 32+42 |
∵∠BCE+∠CBE=90°，∠BCE+∠DCP=90°
∴∠CBE=∠DCP，
又∵∠BEC=∠D=90°，
∴△BEC∽△CDP，
∴
| BE |
| CD |
| BC |
| PC |
∴BE=
| BC |
| PC |
| 4 |
| 5 |
| 16 |
| 5 |
点评：本题主要考查了运用勾股定理的能力，用到的知识点有相似三角形的判定及性质，此题属于常考类型题．
练习册系列答案
名师伴你成长课时同步学练测系列答案
相关题目
、M、C为顶点的三角形与△ABP相似．（请注意：全等图形是相似图形的特例）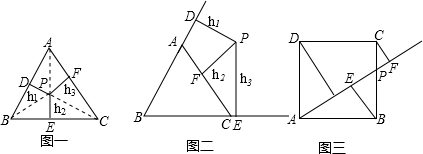
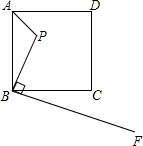
如图，已知点P是边长为4的正方形ABCD内的一点，且PB=3，BF⊥BP，若在射线BF有一点M，使以点B，M，C为顶点的三角形与△ABP相似，那么BM=
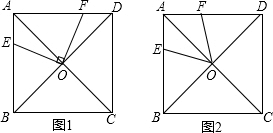
21、如图，已知点P是边长为4的正方形ABCD内一点，且PB=3，BF⊥BP，垂足是B．