Question

如图，已知点P是边长为4的正方形ABCD内一点，且PB=3，BF⊥BP，垂足是B．请在射线BF上找一点M，使以点B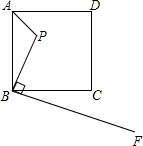、M、C为顶点的三角形与△ABP相似．（请注意：全等图形是相似图形的特例）

Answer 1

分析：此题有两种情况，（1）当△CBM≌△ABP时，全等图形是相似图形的特例，此时BP和BM为一组对应边且相等，BM=BP=3；（2）当△MBC∽△ABP时，有MB：AB=BC：BP，从而求出BM的值．

解答：解：在射线BF上截取线段BM1=

16

3

，连接M₁C，

AB=BC=4 BP=3 BM1= 16 3

?

BM1

AB

=

16 3

4

=

4

3

=

BC

BP

，

BF⊥BP AB⊥BC

?∠ABP=∠CBM₁，
∴△M₁BC∽△ABP．
在射线BF上截取线段BM₂=BP=3，连接M₂C，

AB=BC=4 ∠ABP=∠CBM2 BP=BM2=3

?△CBM₂≌△ABP．（全等必相似）
∴在射线BF上取BM1=

16

3

或BM₂=3时，M₁，M₂都为符合条件的M．
（说明：其他解法请参照给分）

点评：此题主要是考查三角形相似的判定，属中等难度．