题目内容
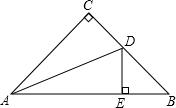 如图所示,在Rt△ABC中,∠C=90°,AC=BC,AD是∠BAC的平分线,DE⊥AB,垂足为E.求证:△DBE的周长等于AB.
如图所示,在Rt△ABC中,∠C=90°,AC=BC,AD是∠BAC的平分线,DE⊥AB,垂足为E.求证:△DBE的周长等于AB.考点:角平分线的性质,等腰直角三角形
专题:证明题
分析:如图,证明DC=DE;进而证明BC=AE,即可解决问题.
解答: 证明:∵∠C=90°,AD是∠BAC的平分线,DE⊥AB,
证明:∵∠C=90°,AD是∠BAC的平分线,DE⊥AB,
∴DC=DE;
∴BD+DE=BD+CD=BC;
∵AC2=AD2-CD2,AE2=AD2-DE2,
∴AC=AE,而AC=BC,
∴BC=AE,
∴BD+DE+BE=AE+BE=AB,
即△DBE的周长等于AB.
 证明:∵∠C=90°,AD是∠BAC的平分线,DE⊥AB,
证明:∵∠C=90°,AD是∠BAC的平分线,DE⊥AB,∴DC=DE;
∴BD+DE=BD+CD=BC;
∵AC2=AD2-CD2,AE2=AD2-DE2,
∴AC=AE,而AC=BC,
∴BC=AE,
∴BD+DE+BE=AE+BE=AB,
即△DBE的周长等于AB.
点评:该题主要考查了角平分线的性质、勾股定理及其应用问题;解题的关键是灵活运用有关定理来分析、判断、推理或解答.

练习册系列答案
相关题目
函数y=
(k≠0)的图象经过点(1,3),那么函数y=(2-k)x的图象经过( )
| k |
| x |
| A、一三象限 | B、二四象限 |
| C、一二象限 | D、三四象限 |
 如图,利用一面墙(墙的长度不限),用20米长的篱笆围成一个矩形的花圃,设AB=x,矩形的面积为y.
如图,利用一面墙(墙的长度不限),用20米长的篱笆围成一个矩形的花圃,设AB=x,矩形的面积为y.(1)求y与x之间的关系式.
(2)求怎样围成一个面积为50m2的矩形花圃?
(3)求出围成矩形最大面积.
 如图,数轴上的两点A,B分别表示实数a,b,则下列四个数a,b,
如图,数轴上的两点A,B分别表示实数a,b,则下列四个数a,b,| 1 |
| a |
| 1 |
| b |
A、
| ||
| B、b | ||
C、
| ||
| D、a |
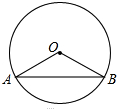 如图,⊙O的半径OA=2,AB是⊙O的一条弦,且AB=2
如图,⊙O的半径OA=2,AB是⊙O的一条弦,且AB=2 武汉晚报上有一个正方移动的广告银幕(正方形ABCD),如图所示,其边长为60cm,点E、F、F、H分别位于正方形ABCD的四条边上,正方形ABCD被分成四个完全一样的直角三角形和一个小正方形EFGH,在一个直角三角形上刊登广告的费用为0.2元/cm2天,在正方形EFGH上刊登广告的费用为0.1元/cm2天,设AE=x(cm),正方形EFGH的面积为s(cm2),一天的总广告费总是w(元).
武汉晚报上有一个正方移动的广告银幕(正方形ABCD),如图所示,其边长为60cm,点E、F、F、H分别位于正方形ABCD的四条边上,正方形ABCD被分成四个完全一样的直角三角形和一个小正方形EFGH,在一个直角三角形上刊登广告的费用为0.2元/cm2天,在正方形EFGH上刊登广告的费用为0.1元/cm2天,设AE=x(cm),正方形EFGH的面积为s(cm2),一天的总广告费总是w(元).