题目内容
函数y=
(k≠0)的图象经过点(1,3),那么函数y=(2-k)x的图象经过( )
| k |
| x |
| A、一三象限 | B、二四象限 |
| C、一二象限 | D、三四象限 |
考点:一次函数图象与系数的关系,反比例函数图象上点的坐标特征
专题:
分析:先把点(1,3)代入函数y=
(k≠0)求出k的值,再把k的值代入函数y=(2-k)x,根据正比例函数的性质即可得出结论.
| k |
| x |
解答:解:∵函数y=
(k≠0)的图象经过点(1,3),
∴3=
,即k=3,
∴当k=3时,函数y=(2-k)x的解析式为y=(2-3)x=-x,
∴此函数的图象经过二、四象限.
故选B.
| k |
| x |
∴3=
| k |
| 1 |
∴当k=3时,函数y=(2-k)x的解析式为y=(2-3)x=-x,
∴此函数的图象经过二、四象限.
故选B.
点评:本题考查的是一次函数的图象与系数的关系,熟知一次函数y=kx(k≠0)中,当k<0时,函数图象经过二、四象限是解答此题的关键.

练习册系列答案
相关题目
已知一个样本27,23,25,27,29,31,27,30,32,28,31,28,26,27,29,18,24,26,27,30,那么频数为8的范围是( )
| A、24.5~26.5 |
| B、26.5~28.5 |
| C、28.5~30.5 |
| D、30.5~32.5 |
 如图,是某月的日历表,在此日历表上可以用一个长方形圈出3×3个位置相邻的9个数(如6,7,8,13,14,15,20,21,22).若被圈出的9个数的和为144,则这9个数中最大的数为( )
如图,是某月的日历表,在此日历表上可以用一个长方形圈出3×3个位置相邻的9个数(如6,7,8,13,14,15,20,21,22).若被圈出的9个数的和为144,则这9个数中最大的数为( )| A、31 | B、26 | C、25 | D、24 |
下列问题中,两个变量成反比例函数的是( )
| A、正方形的周长C与它的边长a |
| B、除数一定,被除数和商 |
| C、三角形的面积一定,一边的长a与这边上的高h |
| D、每支铅笔0.5元,买铅笔的支数与总的价钱 |
 如图,根据图形填空.
如图,根据图形填空.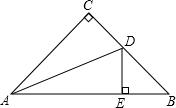 如图所示,在Rt△ABC中,∠C=90°,AC=BC,AD是∠BAC的平分线,DE⊥AB,垂足为E.求证:△DBE的周长等于AB.
如图所示,在Rt△ABC中,∠C=90°,AC=BC,AD是∠BAC的平分线,DE⊥AB,垂足为E.求证:△DBE的周长等于AB. 我国在国际舞台始终注重主动承担国际责任,自2008年12月份起已先后向亚丁湾派出十四批次护航编队,共计四十余艘(次)战舰.2013年6月6日,第十四批护航编队中“微山湖”号综合补给舰从点A处准备靠岸补给休整,然后赶往B点继续执行护航任务,请给出其最佳停靠地点,使其航程最短.
我国在国际舞台始终注重主动承担国际责任,自2008年12月份起已先后向亚丁湾派出十四批次护航编队,共计四十余艘(次)战舰.2013年6月6日,第十四批护航编队中“微山湖”号综合补给舰从点A处准备靠岸补给休整,然后赶往B点继续执行护航任务,请给出其最佳停靠地点,使其航程最短.