题目内容
8. 如图,直线AB:y=x+1与直线CD:y=-2x+4交于点E.
如图,直线AB:y=x+1与直线CD:y=-2x+4交于点E.(1)求E点坐标;
(2)在x轴上找一点F使得FB+FE最小,求OF的长;
(3)若P为直线CD上一点,当△AEP面积为6时,求P的坐标.
分析 (1)联立两个方程解答即可;
(2)作B关于x轴的对称点,得出OF的长;
(3)根据三角形的面积公式解答即可.
解答 解:(1)由题意:$\left\{\begin{array}{l}{y=x+1}\\{y=-2x+4}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$,
所以E(1,2);
(2)作B关于x轴的对称点B1,连接B1E交x轴于F,
∵y=x+1中,B(0,1)
∴B1(-1,0),
设yBE=kx+b(k≠0),
可得:$\left\{\begin{array}{l}{-1=b}\\{2=k+b}\end{array}\right.$,
∴$\left\{\begin{array}{l}{k=3}\\{b=-1}\end{array}\right.$,
∴y=3x-1,
当y=0时,x=$\frac{1}{3}$,
∴OF=$\frac{1}{3}$;
(3)当P在直线AE下方时:${S}_{△APE}={S}_{△ADE}+{S}_{△ADP}=\frac{1}{2}×3×|2-{y}_{P}|=6$,
yP=-2,
所以P1(3,-2),
当P在直线AE上方时:
${S}_{△APE}={S}_{△APD}-{S}_{△ADE}=\frac{1}{2}×3×|{y}_{P}-2|=6$,
yP=6,
所以P2(-1,6)
点评 本题考查了两直线相交或平行问题,关键是由这两条直线相对应的一次函数表达式所组成的二元一次方程组的解分析.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
19. 如图,点E、F、G、H分别在菱形ABCD的四条边上,BE=BF=DG=DH,连接EF,FG,GH,HE,得到四边形EFGH,若AB=a,∠A=60°,当四边形
如图,点E、F、G、H分别在菱形ABCD的四条边上,BE=BF=DG=DH,连接EF,FG,GH,HE,得到四边形EFGH,若AB=a,∠A=60°,当四边形
EFGH的面积取得最大时,BE的长度为( )
 如图,点E、F、G、H分别在菱形ABCD的四条边上,BE=BF=DG=DH,连接EF,FG,GH,HE,得到四边形EFGH,若AB=a,∠A=60°,当四边形
如图,点E、F、G、H分别在菱形ABCD的四条边上,BE=BF=DG=DH,连接EF,FG,GH,HE,得到四边形EFGH,若AB=a,∠A=60°,当四边形EFGH的面积取得最大时,BE的长度为( )
| A. | $\frac{\sqrt{3}a}{3}$ | B. | $\frac{\sqrt{2}a}{2}$ | C. | $\frac{a}{2}$ | D. | $\frac{a}{3}$ |
13.下列方程中,是关于x的一元二次方程的是( )
| A. | ax2+bx+c=0 | B. | $(\frac{1}{x})^{2}+\frac{1}{x}-2=0$ | C. | 3(x+1)2=2(x+1) | D. | 2x2+3x=2x2-2 |
18.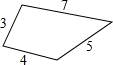 如图,长度分别为3,4,5,7的四条线段首尾相接,相邻两线段的夹角可调整,则任意两端点的距离最大值为( )
如图,长度分别为3,4,5,7的四条线段首尾相接,相邻两线段的夹角可调整,则任意两端点的距离最大值为( )
 如图,长度分别为3,4,5,7的四条线段首尾相接,相邻两线段的夹角可调整,则任意两端点的距离最大值为( )
如图,长度分别为3,4,5,7的四条线段首尾相接,相邻两线段的夹角可调整,则任意两端点的距离最大值为( )| A. | 7 | B. | 9 | C. | 10 | D. | 12 |
 如图,△ABC中,D是BC的中点,DE⊥BC,∠BAC的平分线交DE于E,EF丄AB,EG丄AC于G,连接BE,求证:BF=CG.
如图,△ABC中,D是BC的中点,DE⊥BC,∠BAC的平分线交DE于E,EF丄AB,EG丄AC于G,连接BE,求证:BF=CG. 实数a,b在数轴上的位置如图所示,化简:|a-b|-|b-a|+a=a.
实数a,b在数轴上的位置如图所示,化简:|a-b|-|b-a|+a=a. 已知?ABCD的一组邻边AB、AD的长是关于x的方程x2-4x+m=0的两个实根.
已知?ABCD的一组邻边AB、AD的长是关于x的方程x2-4x+m=0的两个实根.