Question

20．已知?ABCD的一组邻边AB、AD的长是关于x的方程x²-4x+m=0的两个实根．
（1）当m为何值时，四边形ABCD是菱形？
（2）在第（1）问的前提下，若∠ABC=60°，求?ABCD的面积．

Answer 1

分析 （1）四边形ABCD是菱形时，AB=AD，由一元二次方程根的判别式=0即可求出m的值；
（2）连接AC、BD交于点O，由一元二次方程的根求出AB的长，进一步利用菱形的性质和30°角的直角三角形的性质求得对角线的长，利用面积计算方法计算得出答案即可．

解答 解：（1）四边形ABCD是菱形时，AB=AD，
∵AB，AD的长是关于x的方程x²-mx+4=0的两个实数根，
∴△=（-4）²-4m=0，
解得：m=4，
∴当m=4时，四边形ABCD是菱形
（2）如图，连接AC、BD交于点O，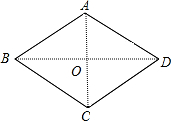

当m=4时，
x²-4x+4=0，
解得：x₁=x₂=2，
则AB=2，
∵四边形ABCD是菱形，∠ABC=60°，
∴∠ABO=$\frac{1}{2}$∠ABC=30°，
D═2OB，AC=2OA，AC⊥BD，
在直角△AOB中，
∵∠ABO=30°，
∴OA=$\frac{1}{2}$AB=1，
0B=$\sqrt{3}$，
BD=2OB=2$\sqrt{3}$，
AC=2OA=2，
∴S_菱形ABCD=$\frac{1}{2}$BD•AC=$\frac{1}{2}$×2×2$\sqrt{3}$=2$\sqrt{3}$．

点评 本题考查了菱形的判定与性质，一元二次方程根的判别式；熟练掌握菱形性质，含30°角的直角三角形的性质，并能进行推理计算是解决问题的关键．