题目内容
14.计算:-2x(x-2)=-2x2+4x.分析 直接利用单项式乘以多项式运算法则求出即可.
解答 解:-2x(x-2)=-2x2+4x.
故答案为:-2x2+4x.
点评 此题主要考查了单项式乘以多项式,正确掌握运算法则是解题关键.

练习册系列答案
相关题目
4.已知二次函数y=ax2+bx+c(a≠0)满足表中条件:
(1)根据表中信息,求出a,b,c的值;
(2)求出(1)中二次函数的图象与x轴的交点坐标;
(3)在(2)中函数的图象与x轴的交点横坐标,若是有理数,请将此函数图象沿x轴平移,使其经过原点;若是无理数,请将此函数图象沿y轴平移(一定不过原点),使其与x轴的交点坐标为有理数,请你只写出上下或左右一次平移即可.
| x | 1 | 0 | -1 |
| bx | -2 | ||
| ax2+bx+c | 1 | 2 |
(2)求出(1)中二次函数的图象与x轴的交点坐标;
(3)在(2)中函数的图象与x轴的交点横坐标,若是有理数,请将此函数图象沿x轴平移,使其经过原点;若是无理数,请将此函数图象沿y轴平移(一定不过原点),使其与x轴的交点坐标为有理数,请你只写出上下或左右一次平移即可.
9.下列实数中,属无理数的是( )
| A. | $\frac{22}{7}$ | B. | 1.010010001 | C. | $\sqrt{27}$ | D. | cos60° |
6.下列二次根式中,最简二次根式是( )
| A. | $\sqrt{8}$ | B. | $\sqrt{169}$ | C. | $\sqrt{{x^2}+4}$ | D. | $\sqrt{\frac{1}{x}}$ |
3.下列代数式中,$\sqrt{x}$+1的一个有理化因式是( )
| A. | $\sqrt{x+1}$ | B. | $\sqrt{x-1}$ | C. | $\sqrt{x}$+1 | D. | $\sqrt{x}$-1 |
4.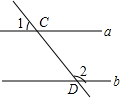 如图,直线a∥b,直线DC与直线a相交于点C,与直线b相交于点D,已知∠1=25°,则∠2的度数为( )
如图,直线a∥b,直线DC与直线a相交于点C,与直线b相交于点D,已知∠1=25°,则∠2的度数为( )
 如图,直线a∥b,直线DC与直线a相交于点C,与直线b相交于点D,已知∠1=25°,则∠2的度数为( )
如图,直线a∥b,直线DC与直线a相交于点C,与直线b相交于点D,已知∠1=25°,则∠2的度数为( )| A. | 135° | B. | 145° | C. | 155° | D. | 165° |
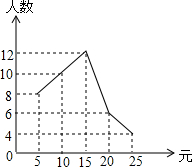 某班40名学生参加了一次“献爱心一日捐”活动,捐款人数与捐款额如图所示,根据图中所提供的信息,你认为这次捐款活动中40个捐款额的中位数是15元.
某班40名学生参加了一次“献爱心一日捐”活动,捐款人数与捐款额如图所示,根据图中所提供的信息,你认为这次捐款活动中40个捐款额的中位数是15元.