题目内容
阅读下列材料:
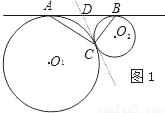
如图1,⊙O1和⊙O2外切于点C,AB是⊙O1和⊙O2外公切线,A、B为切点,
求证:AC⊥BC
证明:过点C作⊙O1和⊙O2的内公切线交AB于D,
∵DA、DC是⊙O1的切线
∴DA=DC.
∴∠DAC=∠DCA.
同理∠DCB=∠DBC.
又∵∠DAC+∠DCA+∠DCB+∠DBC=180°,
∴∠DCA+∠DCB=90°.
即AC⊥BC.
根据上述材料,解答下列问题:
(1)在以上的证明过程中使用了哪些定理?请写出两个定理的名称或内容;
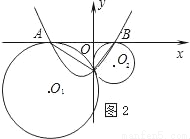
(2)以AB所在直线为x轴,过点C且垂直于AB的直线为y轴建立直角坐标系(如图2),已知A、B两点的坐标为(﹣4,0),(1,0),求经过A、B、C三点的抛物线y=ax2+bx+c的函数解析式;
(3)根据(2)中所确定的抛物线,试判断这条抛物线的顶点是否落在两圆的连心O1O2上,并说明理由.
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目


 -
-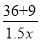 =20 B.
=20 B. 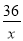 -
-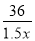 =20 C.
=20 C. 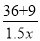 -
-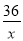 =20 D.
=20 D. 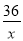 +
+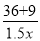 =20
=20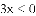
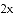
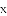

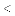
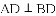
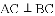
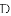
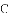
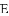
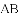
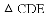
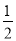 DC.
DC.
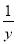 ,﹣
,﹣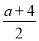 ,
, 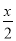 中,是单项式的有( )
中,是单项式的有( )