题目内容
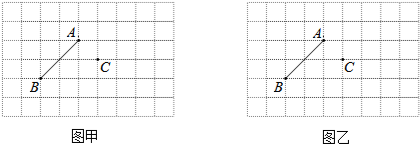
20.如图,在方格纸中,A,B,C三点都在小方格的顶点上,连接AB,按要求画一个以A,B,C为其中三个顶点的平行四边形,并在下方横线上写出所画图形的周长.(每个小方格的边长为1)(1)以AB为边作一个平行四边形,在图甲中画出示意图;
(2)以AB为对角线作一个平行四边形,在图乙中画出示意图.
周长:6$\sqrt{2}$ 周长:2$\sqrt{2}$+2$\sqrt{10}$.
分析 (1)以AB为边作一个平行四边形,由勾股定理求出AB=CD,AC=BD,即可得出周长;
(2)以AB为对角线作一个平行四边形,由勾股定理求出AC=BD,AD=BC,即可得出周长.
解答 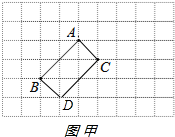 解:(1)以AB为边作一个平行四边形,
解:(1)以AB为边作一个平行四边形,
如图甲所示:
∵AB=CD=$\sqrt{{2}^{2}+{2}^{2}}$=2$\sqrt{2}$,
AC=BD=$\sqrt{{1}^{2}+{1}^{2}}$=$\sqrt{2}$,
∴平行四边形ABDC的周长=2(2$\sqrt{2}$+$\sqrt{2}$)=6$\sqrt{2}$;
故答案为:6$\sqrt{2}$;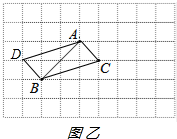 (2)以AB为对角线作一个平行四边形,
(2)以AB为对角线作一个平行四边形,
如图乙所示:
∵AC=BD=$\sqrt{{1}^{2}+{1}^{2}}$=$\sqrt{2}$,
AD=BC=$\sqrt{{3}^{2}+{1}^{2}}$=$\sqrt{10}$,
∴平行四边形ADBC的周长=2$\sqrt{2}$+2$\sqrt{10}$,
故答案为:2$\sqrt{2}$+2$\sqrt{10}$.
点评 本题考查了作图、平行四边形的性质、勾股定理;熟练掌握平行四边形的性质是解决问题的关键.

练习册系列答案
相关题目
10.下列各式由左边到右边的变形,属于因式分解的是( )
| A. | (x+1)(x-1)=x2-1 | B. | x+2x+1=x(x+2)+1 | C. | a2-4b2=(a+2b)(a-2b) | D. | a(x-y)=ax-ay |
9.直角三角形的两边长分别为3和5,则另一边长为( )
| A. | 4 | B. | $\sqrt{41}$ | C. | 4或$\sqrt{34}$ | D. | 4或$\sqrt{41}$ |
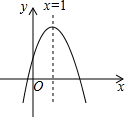 二次函数y=ax2+bx+c(a≠0)图象如图所示,下列结论:
二次函数y=ax2+bx+c(a≠0)图象如图所示,下列结论: 如图,在四边形ABCD中,AD∥BC,∠ABC=90°,E为AD上一点,将△ABE沿直线BE折叠,使点A落在BD上的点G处,延长EG交BC于点F.
如图,在四边形ABCD中,AD∥BC,∠ABC=90°,E为AD上一点,将△ABE沿直线BE折叠,使点A落在BD上的点G处,延长EG交BC于点F.
 如图,在半径为3的⊙O中,直径AB与弦CD相交于点E,连接AC,BD,若AC=2,则cosD=$\frac{1}{3}$.
如图,在半径为3的⊙O中,直径AB与弦CD相交于点E,连接AC,BD,若AC=2,则cosD=$\frac{1}{3}$.