题目内容
已知等腰三角形的一条腰长为25cm，底边长为30cm，求底角的正弦值．
考点：等腰三角形的性质,解直角三角形
专题：
分析：先作底边上的高AD，根据等腰三角形三线合一的性质得到BD=
BC=15cm，再由勾股定理求出AD=
=20cm，然后根据三角函数的定义求解．
| 1 |
| 2 |
| AB2-BD2 |
解答：
解：如图所示：
∵AB=AC=25cm，BC=30cm，AD为底边上的高，
∴BD=
BC=15cm，
由勾股定理得，AD=
=20cm，
∴sin∠ABC=
=
=
．
解：如图所示：∵AB=AC=25cm，BC=30cm，AD为底边上的高，
∴BD=
| 1 |
| 2 |
由勾股定理得，AD=
| AB2-BD2 |
∴sin∠ABC=
| AD |
| AB |
| 20 |
| 25 |
| 4 |
| 5 |
点评：本题考查的是等腰三角形的性质，勾股定理，解直角三角形，熟知锐角三角函数的定义是解答此题的关键．
练习册系列答案
相关题目
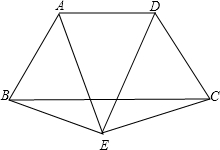如图所示，在等腰梯形ABCD中，AB=CD，AD∥BC，点E是梯形外的一点，且EA=ED，若点F是BC的中点，试判断EF与BC的位置关系，并说明理由．
已知如图，抛物线