题目内容
如图 1,正方形 ABCD 的边长为 4,以 AB 所在的直线为 x 轴,以 AD 所在的直线为 y 轴建立平 面直角坐标系.反比例函数 的图象与 CD 交于 E 点,与 CB 交于 F 点.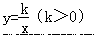
【分析】(1)根据反比例函数图象上点的坐标特点可得出 DE=BF,故可得出结论;
设 DE=BF=a,则 CE=4﹣a,CF=4﹣a,再由 S△AEF=S 正方形 ABCD﹣S△ADE﹣S△ABF﹣S△ECF 即可得出
a 的值,进而可得出反比例函数的解析式;
(3)根据中 EF 两点的坐标用 t 表示出 AB,BG,CE=CK 的长 ,再由 S=S 正方形 ABCD﹣S△梯形 AA′ED
,再由 S=S 正方形 ABCD﹣S△梯形 AA′ED
﹣S△ABG﹣S△ECK 即可得出结论.
【解答】(1)证明:∵点 E、F 均在反比例函数 y= (k>0)的图象上,
(k>0)的图象上,
∴AD•DE=AB•BF.
∵AD=AB,
∴DE=BF.
 在△ADE 与△ABF 中,
在△ADE 与△ABF 中,
,
∴△ADE≌△ABF,
∴AE=AF;
解:设 DE=BF=a,则 CE=4﹣a,CF=4﹣a,
∵△AEF 的面积为 6,
∴S△AEF=S 正方形 ABCD﹣S△ADE﹣S△ABF﹣S△ECF
=4×4﹣ ×4a﹣
×4a﹣ ×4a﹣
×4a﹣ (4﹣a)(4﹣a)
(4﹣a)(4﹣a)
=16﹣4a﹣ (4﹣a)(4﹣a)
(4﹣a)(4﹣a)
=6,
解得 a=2,
∴EF=2×4=8,
∴反比例函数的解析式为 y= ;
;
(3)解:∵由知 E,F(4,2),
∴AB=4﹣t,BG=  AB=2﹣
AB=2﹣  t,CE=CK=2﹣t,
t,CE=CK=2﹣t,
∴S=S 正方形 ABCD﹣S△梯形 AA′ED﹣S△ABG﹣S△ECK
 =4×4﹣
=4×4﹣  ××4﹣
××4﹣  (4﹣t)•﹣
(4﹣t)•﹣
=16﹣4﹣4t﹣  t2﹣4+2t﹣2﹣
t2﹣4+2t﹣2﹣  t2+2t
t2+2t
 =﹣ t2+6.
=﹣ t2+6.


练习册系列答案
 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目
 有意义,那么x的取值范围是____________.
有意义,那么x的取值范围是____________. 
 =0 是关于 x 的一元二次方程,则 k 为 .
=0 是关于 x 的一元二次方程,则 k 为 .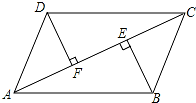
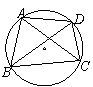
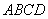 内接于圆,则图中与
内接于圆,则图中与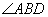 相等的角是( )
相等的角是( )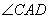 B、
B、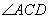 C、
C、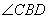 D、
D、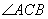
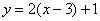 的对称轴是 .
的对称轴是 . B.
B.  C.
C.  D.
D. 
 ,则
,则 的值为_____.
的值为_____.