题目内容
如图,AC 是▱ABCD 的一条对角线,BE⊥AC,DF⊥AC,垂足分别为 E,F.
(1)求证:△ADF≌△CBE; 求证:四边形 DFBE 是平行四边形.
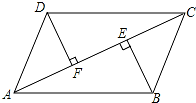
【考点】平行四边形的判定与性质;全等三角形的判定与性质.
【专题】证 明题.
明题.
【分析】(1)由平行四边形的性质得出 AD∥BC,AD=BC,得出内错角相等∠DAF=∠BCE,证出
∠AFD=∠CEB=90°,由 AAS 证明△ADF≌△CBE 即可; 由(1)得:△ADF≌△CBE,由全等三角形的性质得出 DF=BE,再由 BE∥DF,即可得出四边形 DFBE 是平行四边形.
【解答】(1)证明:∵四边形 ABCD 是平行四边形,
∴AD∥BC,AD=BC,
∴∠DAF=∠BCE,
∵BE⊥AC,DF⊥AC,
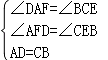 ∴BE∥DF,∠AFD=∠CEB=90°,
∴BE∥DF,∠AFD=∠CEB=90°,
在△ADF 和△CBE 中, ,
∴:△ADF≌△CBE(AAS); 解:如图所示:由(1)得:△ADF≌△CBE,
∴DF=BE,
∵BE∥DF,
∴四边形 DFBE 是平行四边形.
【点评】本题考查了平行四边形的判定与性质、全等三角形的判定与性质;熟练掌握平行四边形的 性质,证明三角形全 等是解决问题的关键.
等是解决问题的关键.

练习册系列答案
相关题目
 B.
B.
 D.
D.
 ,若
,若 ,则
,则 的度数是 .
的度数是 .
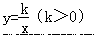
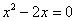 必有实数根
必有实数根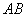 是⊙
是⊙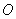 的直径,
的直径, 是⊙
是⊙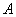 为切点,
为切点,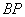 与⊙
与⊙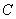 ,点
,点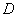 是
是 .
.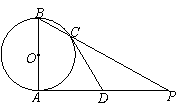 (1)证明:
(1)证明: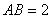 ,
,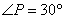 ,求
,求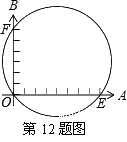 A.10个单位
A.10个单位