题目内容
如图，AD是⊙O的直径，BC与⊙O相切于点B，连结AB、OB、BD，若∠ABC=65°，∠ADB等于（ ）| A、50° | B、55° |
| C、60° | D、65° |
考点：切线的性质
专题：
分析：由BC为圆O的切线，利用切线的性质得到BC垂直于OB，由∠ABC的度数求出∠ABO的度数，再由OA=OB，利用等边对等角得到一对角相等，再利用三角形内角和定理即可求出∠AOB的度数．
解答：解：∵BC为圆O的切线，
∴OB⊥BC，即∠OBC=90°，
∵∠ABC=65°，
∴∠ABO=25°，
∵OA=OB，
∴∠BAO=∠ABO=25°，
∵AD为圆O的直径，
∴∠ABD=90°，
则∠ADB=65°．
故选D
∴OB⊥BC，即∠OBC=90°，
∵∠ABC=65°，
∴∠ABO=25°，
∵OA=OB，
∴∠BAO=∠ABO=25°，
∵AD为圆O的直径，
∴∠ABD=90°，
则∠ADB=65°．
故选D
点评：此题考查了切线的性质，等腰三角形的性质，以及三角形内角和定理，熟练掌握切线的性质是解本题的关键．
练习册系列答案
相关题目
已知圆柱按如图所示方式放置，其左视图的面积为48，则该圆柱的侧面积为
如图，二次函数y=ax2+bx+c的图象与y轴负半轴相交，其顶点为（| 1 |
| 2 |
①ac＜0；②a+b+c＜0；③a-b+c＜0；④a+b=0；⑤b2=4ac+4a．
其中正确的结论有（ ）
| A、5个 | B、4个 | C、3个 | D、2个 |
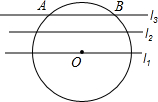如图，在同一平面内，有一组平行线l1、l2、l3，相邻两条平行线之间的距离均为3．点O在直线l1上，⊙O与直线的交点为A、B．且AB=8，则⊙O的半径
如图，在四边形ABCD中，AB=4，CD=13，DE=12，∠DAB=∠DEC=90°，∠ABE=135°，四边形ABCD的面积是（ ）| A、94 | B、90 | C、84 | D、78 |
如图，点B在∠CAD的平分线上，若添加一个适当的条件能使△ABC≌△ABD，所添加的条件不可以是（ ）| A、∠C=∠D |
| B、AC=AD |
| C、∠CBE=∠DBE |
| D、BC=BD |
