题目内容
 如图,在四边形ABCD中,AB=4,CD=13,DE=12,∠DAB=∠DEC=90°,∠ABE=135°,四边形ABCD的面积是( )
如图,在四边形ABCD中,AB=4,CD=13,DE=12,∠DAB=∠DEC=90°,∠ABE=135°,四边形ABCD的面积是( )| A、94 | B、90 | C、84 | D、78 |
考点:勾股定理
专题:
分析:连接DB,延长AB和DE交于F,设BE=x,先由勾股定理,得DB2=x2+122,AD2=x2+128,再证明△BEF是等腰直角三角形,得出EF=BE=x,BF=
x,然后在直角△ADF中,根据勾股定理得出AD2+AF2=DF2,由此列出关于x的方程,解方程求出x的值,则四边形ABCD的面积=△ABD的面积+△BCE的面积.
| 2 |
解答: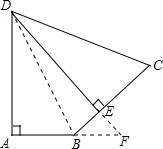 解:连接DB,延长AB和DE交于F,设BE=x,
解:连接DB,延长AB和DE交于F,设BE=x,
由勾股定理,得DB2=BE2+DE2=x2+122,
AD2=DB2-AB2=x2+122-42=x2+128.
∵∠ABE=135°,
∴∠EBF=45°,
又∵∠BEF=90°,
∴EF=BE=x,BF=
x.
在△ADF中,∵∠DAF=90°,
∴AD2+AF2=DF2,
即x2+128+(4+
x)2=(12+x)2,
∴3x2+8
x+144=x2+24x+144,
2x2=(24-8
)x,
∵x≠0,
∴x=12-4
,
∴AD2=(12-4
)2+128=304-96
,
∴AD=12
-4.
∴四边形ABCD的面积=△ABD的面积+△BCE的面积
=
AB•AD+
(BE+EC)•DE
=
×4(12
-4)+
(12-4
+5)×12
=94.
故选A.
 解:连接DB,延长AB和DE交于F,设BE=x,
解:连接DB,延长AB和DE交于F,设BE=x,由勾股定理,得DB2=BE2+DE2=x2+122,
AD2=DB2-AB2=x2+122-42=x2+128.
∵∠ABE=135°,
∴∠EBF=45°,
又∵∠BEF=90°,
∴EF=BE=x,BF=
| 2 |
在△ADF中,∵∠DAF=90°,
∴AD2+AF2=DF2,
即x2+128+(4+
| 2 |
∴3x2+8
| 2 |
2x2=(24-8
| 2 |
∵x≠0,
∴x=12-4
| 2 |
∴AD2=(12-4
| 2 |
| 2 |
∴AD=12
| 2 |
∴四边形ABCD的面积=△ABD的面积+△BCE的面积
=
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
| 2 |
| 1 |
| 2 |
| 2 |
=94.
故选A.
点评:本题考查了勾股定理,邻补角的性质,等腰直角三角形的判定与性质,三角形的面积,有一定难度.正确作出辅助线.利用方程思想是解题的关键.

练习册系列答案
相关题目
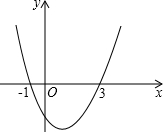 二次函数y=ax2+bx+c的图象如图所示,则下列说法中正确的是( )
二次函数y=ax2+bx+c的图象如图所示,则下列说法中正确的是( )| A、ac>0 |
| B、4a+2b+c>0 |
| C、当x>1时,y随x的增大而减小 |
| D、a+b<m(am+b)(m≠1) |
 如图,AD是⊙O的直径,BC与⊙O相切于点B,连结AB、OB、BD,若∠ABC=65°,∠ADB等于( )
如图,AD是⊙O的直径,BC与⊙O相切于点B,连结AB、OB、BD,若∠ABC=65°,∠ADB等于( )| A、50° | B、55° |
| C、60° | D、65° |
 一条排水管的截面如图所示.已知排水管的截面圆半径OB=10,水面宽AB=16,则水管中水的最大深度是( )
一条排水管的截面如图所示.已知排水管的截面圆半径OB=10,水面宽AB=16,则水管中水的最大深度是( )| A、4 | B、6 | C、8 | D、10 |
以数形结合的观点解题,方程x2+x-1=0的实根可看成函数y=x2与函数y=1-x的图象交点的横坐标,也可以看成函数y=x+1与函数y=
的图象交点的横坐标,那么用此方法可推断方程x3+x-1=0的一个实根x的所在范围是( )
| 1 |
| x |
A、-
| ||
B、0<x<
| ||
C、
| ||
D、1<x<
|
 九年级(1)班和(2)班各选派了七位学生参加一次科普知识竞赛,他们的成绩分别如下表:
九年级(1)班和(2)班各选派了七位学生参加一次科普知识竞赛,他们的成绩分别如下表: 如图,在矩形ABCD中,AB=2,AD=4,将矩形ABCD沿直线EF折叠,D到G得位置,C到H得位置,BC交EG于M点.则图中四边形ABME和四边形GHFM的周长和是( )
如图,在矩形ABCD中,AB=2,AD=4,将矩形ABCD沿直线EF折叠,D到G得位置,C到H得位置,BC交EG于M点.则图中四边形ABME和四边形GHFM的周长和是( )