��Ŀ����
5����PΪ��ABC��һ�㣬�����PAC=��PBC����ô���dzƵ�PΪ��ABC����A��B�ĵȽǵ㣮��1����ͼ1���ڡ�ABC�У�AC=BC��PA=PB����֤��P�ǡ�ABC����A��B�ĵȽǵ㣻
��2����ͼ2���ڡ�ABC�У�AC=BC����D��AB�ߵ��е㣬��PΪ��ABC����A��B�ĵȽǵ㣬PE��BC�ڵ�E��PF��AC�ڵ�F����֤��DE=DF��
��3����ͼ3�������ڣ�2���еġ�AC=BC���ijɡ�AC��BC���������������䣬��֤��DE=DF��
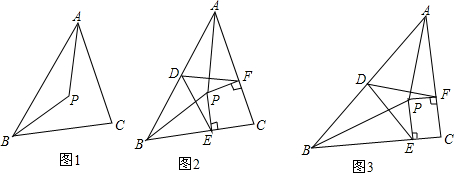
���� ��1�����ݵ��������ε����ʼ��ɵõ������
��2��ͨ����PFA�ա�PEB �͡�DFA�ա�DEB���Ϳ��õ����ۣ�
��3���ֱ�ȡPA��PB���е�M��N������FM��DM��DN��NE����P�ǡ�ABC����A��B�ĵȽǵ㣬�õ���PAC=��PBC����PMF=��PNE������DM��DN���ǡ�PAB����λ�ߣ��Ƴ�DM��BP��DM=$\frac{1}{2}$BP��DN��$\frac{1}{2}$AP��DN=$\frac{1}{2}$AP������DM=$\frac{1}{2}$BP��EN=$\frac{1}{2}BP$��DN=$\frac{1}{2}$AP��MF=$\frac{1}{2}AP$���õ�DM=EN��DN=MF�����ݡ�DMF�ա�DNE���õ�����DF=DE��
��� ��1��֤����AC=BC��
���CAB=��CBA��
��PA=PB��
���PAB=��PBA��
���PBC=��PAC��
��P�ǡ�ABC����A��B�ĵȽǵ㣻
��2��֤����P�ǡ�ABC����A��B�ĵȽǵ㣬
���PAC=��PBC��
��AC=BC��
���BAC=��ABC��
���PAB=��PBA��
��PA=PB��
��PF��AC��PE��BC��
���PFA=��PEB
�ߡ�PBC=��PAC��PA=PB��
�ڡ�PFA���PEB �У�
$\left\{\begin{array}{l}{��PFA=��PEB}\\{��PBA=��PAC}\\{PA=PB}\end{array}\right.$��
���PFA�ա�PEB��
��FA=EB
�ߵ�D��AB���е㣬
��AD=BD��
�ߡ�BAC=��ABC��FA=EB��
�ڡ�DFA���DEB�У�
$\left\{\begin{array}{l}{AD=BD}\\{��BAC=ABC}\\{FA=EB}\end{array}\right.$��
���DFA�ա�DEB��
��DF=DE��
��3��֤�����ֱ�ȡPA��PB���е�M��N������FM��DM��DN��NE��
�ߡ�AFP=��BEP=90�㣬
��MF=AM=$\frac{1}{2}AP$��EN=BM=$\frac{1}{2}BP$��
���PAC=��AFM����PAE=��BEN��
���PMF=2��PAC����PNE=2��PBC��
��P�ǡ�ABC����A��B�ĵȽǵ㣬
���PAC=��PBC��
���PMF=��PNE��
��DM��DN���ǡ�PAB����λ�ߣ�
��DM��BP��DM=$\frac{1}{2}$BP��DN��$\frac{1}{2}$AP��DN=$\frac{1}{2}$AP��
���DMP+��APB=180�㣬��DNP+��APB=180�㣬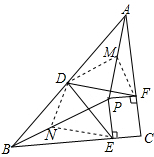
���DMP=��DNP��
�ߡ�PMF=��PNE��
���DMF=��DNE��
��DM=$\frac{1}{2}$BP��EN=$\frac{1}{2}BP$��DN=$\frac{1}{2}$AP��MF=$\frac{1}{2}AP$��
��DM=EN��DN=MF��
�ڡ�DMF���DNE�У�
$\left\{\begin{array}{l}{DM=EN}\\{��DMF=DNE}\\{MF=DN}\end{array}\right.$��
���DMF�ա�DNE��
��DF=DE��
���� ���⿼����ȫ���������ж������ʣ����������ε����ʣ������ε���λ�߶�������ȷ�������������ǽ���Ĺؼ���

 ȫ�ܲ����ĩС״Ԫϵ�д�
ȫ�ܲ����ĩС״Ԫϵ�д� ��Ȥ����¹�֪��ϵ�д�
��Ȥ����¹�֪��ϵ�д�| A�� | x��2 | B�� | x��2 | C�� | x��2 | D�� | x��-2 |
| A�� | ��2�α���1�����泯�� | B�� | ����5�����泯�� | ||
| C�� | ������5�����泯�� | D�� | ������10�����泯�� |
| A�� | a2•a3=a6 | B�� | $\sqrt{6}$��$\sqrt{2}$=$\sqrt{3}$ | C�� | ��$\frac{1}{2}$��-2=-2 | D�� | ��-a3��2=-a6 |



