题目内容

15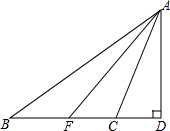．如图所示，AD、AF分别是△ABC的高和角平分线，已知∠B=36°，∠ACB=104°，求∠DAF的度数．

分析 先根据△ACB中，∠B=36°，∠ACB=104°求出∠BAC的度数，再由AF是∠BAC的角平分线求出∠BAF的度数，再由三角形外角的性质得出∠AFD的度数，由三角形内角和定理即可得出结论．

解答 解：∵△ACB中，∠B=36°，∠ACB=104°，
∴∠BAC=180°-104°-36°=40°．
∵AF是∠BAC的角平分线，
∴∠BAF=20°，
∴∠AFD=∠B+∠BAF=36°+20°=56°．
在△AFD中，
∵AD⊥BD，
∴∠D=90°，
∴∠DAF=90°-∠AFD=90°-56°=34°．

点评 本题考查的是三角形内角和定理，熟知三角形内角和是180°是解答此题的关键．

练习册系列答案
相关题目
2．某市为处理污水，需要铺设一条长为5000m的管道，为了尽量减少施工对交通所造成的影响，实际施工时每天比原计划多铺设20m，结果提前15天完成任务．设原计划每天铺设管道x m，则可得方程$\frac{5000}{x}$-$\frac{5000}{x+20}$=15．
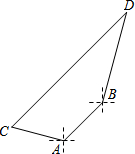6．在海岸A处，发现北偏东45°方向、距离A处20海里的B处有一艘走私船；在A处北偏西75°方向、距离A处20海里的C处的缉私船奉命以10$\sqrt{3}$海里/小时的速度追截走私船．同时，走私船正以10海里/小时的速度从B处向北偏东15°方向逃窜，问缉私船沿什么方向能最快追上走私船？最少要花多少时间？
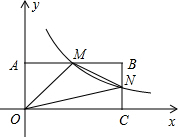3．如图，在直角坐标系中，矩形OABC的顶点O与坐标原点重合，A、C分别在坐标轴上，点B的坐标为（4，2），直线y=-$\frac{1}{2}$x+3交AB，BC分别于点M，N，反比例函数y=$\frac{k}{x}$的图象经过点M，N．
（1）求点M，N的坐标；
（2）求反比例函数的解析式；
（3）求四边形BMON的面积S；
（4）若点P在y轴上，且△OPM的面积与四边形BMON的面积相等，求点P的坐标．
10．如图，直线AB分别交EF、BC于点A、B，AC平分∠BAE，∠ABC=76°，∠GAF=52°，EF与BC平行吗？请说明理由．
20．如图所示的网格中各有不同的图案，不能通过平移得到的是（　　）
A．B．C．D．
7．下列计算中，正确的是（　　）
A．（-5）-（-3）=-8B．（+5）-（3）=2C．（+7）-（+8）=-1D．（-5）-|-5|=0
4．阅读下面材料，并解答问题．
材料：将分式$\frac{-{x}^{4}-{x}^{2}+3}{-{x}^{2}+1}$拆分成一个整式与一个分式（分子为整数）的和的形式
解：由于分母为-x2+1，可设-x4-x2+3=（-x2+1）（x2+a）+b
∴-x4-x2+3=-x4-ax2+x2+a+b∴-x4-x2+3=-x4-（a-1）x2+（a+b）
∵对于任意x，上述等式均成立，∴$\left\{\begin{array}{l}{a-1=1}\\{a+b=3}\end{array}\right.$∴$\left\{\begin{array}{l}{a=2}\\{b=1}\end{array}\right.$
∴$\frac{-{x}^{4}-{x}^{2}+3}{-{x}^{2}+1}$=$\frac{（-{x}^{2}+1）（{x}^{2}+2）+1}{-{x}^{2}+1}$=$\frac{（-{x}^{2}+1）（{x}^{2}+2）}{-{x}^{2}+1}$+$\frac{1}{-{x}^{2}+1}$=x2+2+$\frac{1}{-{x}^{2}+1}$
这样，分式$\frac{-{x}^{4}-{x}^{2}+3}{-{x}^{2}+1}$被拆分成了一个整式x2+2与一个分式$\frac{1}{-{x}^{2}+1}$的和
阅读上面的材料后，请你解答下列问题
（1）将分式$\frac{{x}^{4}-4{x}^{2}-4}{{x}^{2}+1}$拆分成一个整式与一个分式（分子为整数）的和的形式．
（2）试说明$\frac{{x}^{4}-4{x}^{2}-4}{{x}^{2}+1}$的最小值为-4．
5．（1）计算：（$\sqrt{3}$）2-$\sqrt{（-1）^{2}}$                   
（2）解方程：2x2-2x=3．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网