题目内容
7.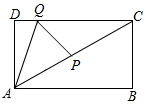 如图,长方形ABCD中,AD=a,DC=b,(a,b为常数),∠CAB=30°,点P是对角线AC的中点,点Q是线段CD上的动点,则AQ+QP的最小值为$\sqrt{3}a$.
如图,长方形ABCD中,AD=a,DC=b,(a,b为常数),∠CAB=30°,点P是对角线AC的中点,点Q是线段CD上的动点,则AQ+QP的最小值为$\sqrt{3}a$.
分析 根据图形和题意,作点P关于直线CD的对称点P′,然后根据两点之间线段最短,可以解答本题.
解答 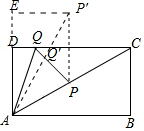 解:作点P关于直线CD的对称点P′,如右图所示,
解:作点P关于直线CD的对称点P′,如右图所示,
∵长方形ABCD中,AD=a,DC=b,(a,b为常数),∠CAB=30°,点P是对角线AC的中点,
∴AE=a+0.5a=1.5a,EP′=0.5b,tan30°=$\frac{a}{b}=\frac{\sqrt{3}}{3}$,
∴b=$\sqrt{3}a$,
∵两点之间线段最短,
∴AQ+QP的最小值就是线段AP′的长度,
∵∠AEP′=90°,EP′=0.5b,AE=1.a,
∴AP′=$\sqrt{(0.5b)^{2}+(1.5a)^{2}}$=$\frac{\sqrt{9{a}^{2}+{b}^{2}}}{2}$=$\frac{\sqrt{9{a}^{2}+3{a}^{2}}}{2}=\frac{\sqrt{12{a}^{2}}}{2}=\frac{2\sqrt{3}a}{2}$=$\sqrt{3}a$,
故答案为:$\sqrt{3}a$.
点评 本题考查轴对称-最短路径问题、矩形的性质、勾股定理,解答本题的关键是明确题意,找出所求问题需要的条件,利用勾股定理和锐角三角函数解答.

练习册系列答案
相关题目
17.点A(2,-1)关于x轴对称的点B的坐标为( )
| A. | (2,1) | B. | (-2,1) | C. | (2,-1) | D. | (-2,-1) |
18.在Rt△ABC中,∠C=90°,∠A的对边为a,∠B的对边为b,且满足a2-ab-b2=0,则tanA=( )
| A. | 1 | B. | $\frac{1+\sqrt{5}}{2}$ | C. | $\frac{1-\sqrt{5}}{2}$ | D. | $\frac{1±\sqrt{5}}{2}$ |
19.下列多项式中,各项系数的积是30的是( )
| A. | -x2+5x+6 | B. | 2x2+2x-5 | C. | $\frac{{4{x^2}-20x-3}}{2}$ | D. | -32x+$\frac{2}{3}$y+5z |
 如图,AB∥CD,AC、BC相交于点E,∠B=52°,求∠C.
如图,AB∥CD,AC、BC相交于点E,∠B=52°,求∠C.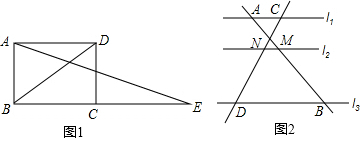
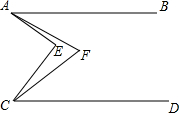 如图,已知AB∥CD,∠EAF=$\frac{1}{4}$∠EAB,∠ECF=$\frac{1}{4}$∠ECD,求证:∠AFC=∠$\frac{3}{4}$AEC.
如图,已知AB∥CD,∠EAF=$\frac{1}{4}$∠EAB,∠ECF=$\frac{1}{4}$∠ECD,求证:∠AFC=∠$\frac{3}{4}$AEC.