题目内容
如图，OD、OE分别是∠AOC的平分线，∠AOD=40°，∠BOE=25°，求∠AOB的度数．
解：因为OD平分∠AOC，OE平分∠BOC（已知）．
所以∠AOC=2∠AOD，∠BOC=2________，
因为∠AOD=40°，________=25°（已知）
所以∠AOC=2×40°=80°（等量代换），
∠BOC=2×________=________．
所以∠AOB=________．
∠BOE ∠BOE 25° 50° 130°
分析：根据角平分线定义得出∠AOC=2∠AOD，∠BOC=2∠BOE，求出∠AOC=80°，∠BOC=50°，相加即可．
解答：∵OD平分∠AOC，OE平分∠BOC，
∴∠AOC=2∠AOD，∠BOC=2∠BOE，
∵∠AOD=40°，∠BOE=25°，
∴∠AOC=2×40°=80°，∠BOC=2×25°=50°，
∴∠AOB=80°+50°=130°，
故答案为：∠BOE，∠BOE，25°，50°，130°．
点评：本题考查了角平分线定义的应用，主要考查学生的计算能力．
分析：根据角平分线定义得出∠AOC=2∠AOD，∠BOC=2∠BOE，求出∠AOC=80°，∠BOC=50°，相加即可．
解答：∵OD平分∠AOC，OE平分∠BOC，
∴∠AOC=2∠AOD，∠BOC=2∠BOE，
∵∠AOD=40°，∠BOE=25°，
∴∠AOC=2×40°=80°，∠BOC=2×25°=50°，
∴∠AOB=80°+50°=130°，
故答案为：∠BOE，∠BOE，25°，50°，130°．
点评：本题考查了角平分线定义的应用，主要考查学生的计算能力．
练习册系列答案
相关题目
如图，∠AOB=60°，OD、OE分别平分∠BOC、∠AOC，那么∠EOD=
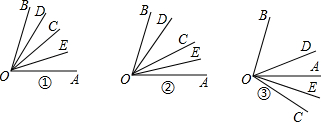
如图，已知∠AOB=2∠BOC，又OD，OE分别为∠AOB和∠BOC的平分线，若∠DOE=66°．
