题目内容
16.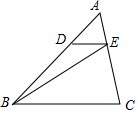 如图,△ABC中,D、E分别是边AB、AC 上的点,且∠DEB=∠EBC.
如图,△ABC中,D、E分别是边AB、AC 上的点,且∠DEB=∠EBC.(1)求证:△ADE∽△ABC;
(2)若EC=2AE,求△ADE和△BEC的面积之比.
分析 (1)由平行线的判定与性质推知DE∥BC,结合平行线的性质和相似三角形的判定定理进行证明;
(2)利用相似三角形的面积之比等于相似比得到S△ADE:S△ABC=1:9,所以S△ADE:S△DBE=1:2,故△ADE和△BEC的面积比=1:6.
解答  (1)解:∵∠DEB=∠EBC,
(1)解:∵∠DEB=∠EBC,
∴DE∥BC,
∴∠AED=∠ACB且∠A=∠A,
∴△ADE∽△ABC;
(2)∵AE:EC=1:2,
∴AE:AC=1:3
∴S△ADE:S△ABC=1:9,
∴S△ADE:S△DBE=1:2,
∴△ADE和△BEC的面积比=1:6.
点评 本题考查了相似三角形的判定与性质.本题关键是要懂得找相似三角形,利用相似三角形的性质求解.

练习册系列答案
相关题目
7.一列数:0,1,2,3,6,7,14,15,30、这串数是由小明按照一定规则写下来的,他第一次写下“0,1”,第二次接着写“2,3”,第三次接着写“6,7”,第四次接着写“14,15”,就这样一直接着往下写,那么这串数接下来的三个数应该是下面的( )
| A. | 30,32,64 | B. | 31,62,63 | C. | 31,32,33 | D. | 31,45,46 |
5. 如图,△ACB≌△DCE,∠BCE=25°,则∠ACD的度数为( )
如图,△ACB≌△DCE,∠BCE=25°,则∠ACD的度数为( )
 如图,△ACB≌△DCE,∠BCE=25°,则∠ACD的度数为( )
如图,△ACB≌△DCE,∠BCE=25°,则∠ACD的度数为( )| A. | 20° | B. | 25° | C. | 30° | D. | 35° |
 如图,已知AF∥EC,AB∥CD,∠A=65°,则∠C=65度.
如图,已知AF∥EC,AB∥CD,∠A=65°,则∠C=65度.
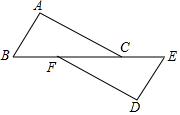 已知:如图,点B、F、C、E在一条直线上,∠B=∠E,∠ACB=∠DFE,且BF=EC.求证:△ABC≌△DEF.
已知:如图,点B、F、C、E在一条直线上,∠B=∠E,∠ACB=∠DFE,且BF=EC.求证:△ABC≌△DEF.