题目内容
 如图,Rt△ABC中,∠C=90°,AC=3,BC=4,以C点为圆心,CA为半径的圆与AB,BC分别交于点D,E,则弦AD的长为
如图,Rt△ABC中,∠C=90°,AC=3,BC=4,以C点为圆心,CA为半径的圆与AB,BC分别交于点D,E,则弦AD的长为考点:垂径定理,勾股定理
专题:
分析:先根据勾股定理求出AB的长,过C作CM⊥AB,交AB于点M,由垂径定理可知M为AD的中点,由三角形的面积可求出CM的长,在Rt△ACM中,根据勾股定理可求出AM的长,进而可得出结论.
解答: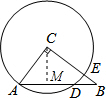 解:∵在Rt△ABC中,∠ACB=90°,AC=3,BC=4,
解:∵在Rt△ABC中,∠ACB=90°,AC=3,BC=4,
∴AB=
=
=5,
过C作CM⊥AB,交AB于点M,如图所示,
∵CM⊥AB,
∴M为AD的中点,
∵S△ABC=
AC•BC=
AB•CM,且AC=3,BC=4,AB=5,
∴CM=
,
在Rt△ACM中,根据勾股定理得:AC2=AM2+CM2,即9=AM2+(
)2,
解得:AM=
,
∴AD=2AM=
.
故答案为:
.
 解:∵在Rt△ABC中,∠ACB=90°,AC=3,BC=4,
解:∵在Rt△ABC中,∠ACB=90°,AC=3,BC=4,∴AB=
| AC2+BC2 |
| 32+42 |
过C作CM⊥AB,交AB于点M,如图所示,
∵CM⊥AB,
∴M为AD的中点,
∵S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
∴CM=
| 12 |
| 5 |
在Rt△ACM中,根据勾股定理得:AC2=AM2+CM2,即9=AM2+(
| 12 |
| 5 |
解得:AM=
| 18 |
| 5 |
∴AD=2AM=
| 36 |
| 5 |
故答案为:
| 36 |
| 5 |
点评:本题考查的是垂径定理,根据题意作出辅助线,构造出直角三角形是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
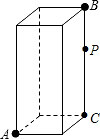 如图,是一长、宽都是3cm,高BC=9cm的长方体纸箱,BC上有一点P,PC=
如图,是一长、宽都是3cm,高BC=9cm的长方体纸箱,BC上有一点P,PC=| 2 |
| 3 |
A、6
| ||
B、3
| ||
| C、10cm | ||
| D、12cm |
若a>b,则下列不等式中一定成立的是( )
A、
| ||
B、
| ||
| C、-a>-b | ||
| D、a-b>0 |
将二次函数y=-2x2的图象平移后,可得到二次函数y=-2(x+1)2的图象,平移的方法是( )
| A、向上平移1个单位 |
| B、向下平移1个单位 |
| C、向左平移1个单位 |
| D、向右平移1个单位 |
 如图,为吉林省农安县城内的一座辽代古塔,为了实现测量古塔外墙底部墙角∠ABC的度数,请你运用所学过的知识设计两种测量方案,并说明理由.
如图,为吉林省农安县城内的一座辽代古塔,为了实现测量古塔外墙底部墙角∠ABC的度数,请你运用所学过的知识设计两种测量方案,并说明理由.