题目内容
10.如图,用棋子按照一定规律摆出下列一组图形,则第n个图形的棋子的个数是n2+4n+6(用含n的代数式表示).
分析 将图形拆分成两个图形,上面看做一个“八”,下面看做一个正方形,分别总结两个图形组成规律即可;
解答 解:观察图形,将图形拆分成两个图形:上面是一个“八”字形,下面是一个正方形,
由已知得:
图1:八字形有3×2+1个,正方形有2×2个,
图2:八字形有4×2+1个,正方形有3×3个,
图3:八字形有5×2+1个,正方形有4×4个,
可以总结规律如下:
图n:八字形有(n+2)×2+1个,正方形有(n+1)×(n+1)个,
合计:(n+2)×2+1+(n+1)×(n+1)=2n+5+n2+2n+1=n2+4n+6.
故答案为:n2+4n+6.
点评 题目考查了图形的变化规律,通过图形变化,总结出变化的一般规律,解决本题的关键就是拆分图形,总结出图形变化规律.

练习册系列答案
相关题目
19.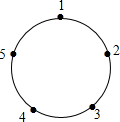 如图,一只青蛙在圆周上标有数字的五个点上跳,若它停在奇数点上,则下列沿顺时针方向跳两个点:若停在偶数点上,则下次沿逆时针方向跳一个点,若青蛙从1这点开始跳,则经过2016次后它停在哪个数对应的点上( )
如图,一只青蛙在圆周上标有数字的五个点上跳,若它停在奇数点上,则下列沿顺时针方向跳两个点:若停在偶数点上,则下次沿逆时针方向跳一个点,若青蛙从1这点开始跳,则经过2016次后它停在哪个数对应的点上( )
 如图,一只青蛙在圆周上标有数字的五个点上跳,若它停在奇数点上,则下列沿顺时针方向跳两个点:若停在偶数点上,则下次沿逆时针方向跳一个点,若青蛙从1这点开始跳,则经过2016次后它停在哪个数对应的点上( )
如图,一只青蛙在圆周上标有数字的五个点上跳,若它停在奇数点上,则下列沿顺时针方向跳两个点:若停在偶数点上,则下次沿逆时针方向跳一个点,若青蛙从1这点开始跳,则经过2016次后它停在哪个数对应的点上( )| A. | 1 | B. | 2 | C. | 3 | D. | 5 |
20.下列函数中,属于二次函数的是( )
| A. | y=2x+1 | B. | y=(x-1)2-x2 | C. | y=2x2-7 | D. | $y=-\frac{1}{x^2}$ |
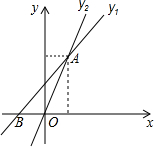 如图,已知一次函数y1=(m-2)x+2与正比例函数y2=2x图象相交于点A(2,n),一次函数y1=(m-2)x+2与x轴交于点B.
如图,已知一次函数y1=(m-2)x+2与正比例函数y2=2x图象相交于点A(2,n),一次函数y1=(m-2)x+2与x轴交于点B.