题目内容
8.计算:(1)($\sqrt{2}$-$\sqrt{3}$)2+2$\sqrt{\frac{1}{3}}$•3$\sqrt{2}$;
(2)(5$\sqrt{48}$-6$\sqrt{27}$+4$\sqrt{15}$)÷$\sqrt{3}$.
分析 (1)根据完全平方公式和二次根式的乘法可以解答本题;
(2)先将除法转化为乘法,再根据乘法的分配律可以解答本题.
解答 解:(1)($\sqrt{2}$-$\sqrt{3}$)2+2$\sqrt{\frac{1}{3}}$•3$\sqrt{2}$
=2-2$\sqrt{6}$+3+2$\sqrt{6}$
=5;
(2)(5$\sqrt{48}$-6$\sqrt{27}$+4$\sqrt{15}$)÷$\sqrt{3}$
=(5$\sqrt{48}$-6$\sqrt{27}$+4$\sqrt{15}$)×$\frac{1}{\sqrt{3}}$
=5$\sqrt{16}$-6$\sqrt{9}$+4$\sqrt{5}$
=20-18+4$\sqrt{5}$
=2+4$\sqrt{5}$.
点评 本题考查二次根式的混合运算,解题的关键是明确二次根式的混合运算的计算方法.

练习册系列答案
相关题目
3.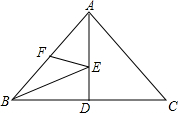 如图,在△ABC中,AB=AC=5,BC=6,AD⊥BC于D,点E,F分别在AD,AB上,则BE+EF的最小值是( )
如图,在△ABC中,AB=AC=5,BC=6,AD⊥BC于D,点E,F分别在AD,AB上,则BE+EF的最小值是( )
 如图,在△ABC中,AB=AC=5,BC=6,AD⊥BC于D,点E,F分别在AD,AB上,则BE+EF的最小值是( )
如图,在△ABC中,AB=AC=5,BC=6,AD⊥BC于D,点E,F分别在AD,AB上,则BE+EF的最小值是( )| A. | 4 | B. | 4.8 | C. | 5 | D. | 5.4 |
18.一组数据 2,-1,0,-2,x,1 的中位数是0,则x等于( )
| A. | -1 | B. | 1 | C. | 0 | D. | -2 |

