题目内容
7.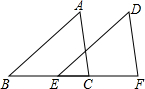 已知:如图,点B、E、C、F在同一条直线上,且AB=DE,AC=DF,BE=CF.求证:AB∥DE.请将下面的过程和理由补充完整
已知:如图,点B、E、C、F在同一条直线上,且AB=DE,AC=DF,BE=CF.求证:AB∥DE.请将下面的过程和理由补充完整解:∵BE=CF已知
∴BE+EC=CF+EC即BC=EF.
在△ABC和△DEF中,
=DE( 已知 )
AC=DF已知
BC=EF
∴△ABC≌△DEFSSS
∴∠ABC=∠DEF全等三角形的对应角相等
∴AB∥DE同位角相等,两直线平行.
分析 根据已知条件,通过全等三角形的判定定理SSS证得△ABC≌△DEF,则全等三角形的对应角相等,利用平行线的判定定理得出AB∥DE.
解答 解:∵BE=CF(已知),
∴BE+EC=CF+EC,即BC=EF,
在△ABC和△DEF中,
AB=DE(已知)
AC=DF(已知)
BC=EF(已证)
∴△ABC≌△DEF(SSS)
∴∠ABC=∠DEF (全等三角形的对应角相等)
∴AB∥DE (同位角相等,两直线平行 ),
故答案为:已知;BC=EF;已知;EF;SSS;全等三角形的对应角相等;同位角相等,两直线平行.
点评 本题考查了全等三角形的判定定理及性质和平行线的判定定理,解题时注意数形结合,掌握全等三角形的判定定理是解答此题的关键.

练习册系列答案
 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
18.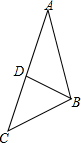 如图,在△ABC中,D是边AC上一点,连接BD,给出下列条件:①∠ABD=∠ACB;②AB2=AD•AC;③∠A=∠ABD;④AB•BC=AC•BD.其中单独能够判定△ABD∽△ACB的个数是( )
如图,在△ABC中,D是边AC上一点,连接BD,给出下列条件:①∠ABD=∠ACB;②AB2=AD•AC;③∠A=∠ABD;④AB•BC=AC•BD.其中单独能够判定△ABD∽△ACB的个数是( )
 如图,在△ABC中,D是边AC上一点,连接BD,给出下列条件:①∠ABD=∠ACB;②AB2=AD•AC;③∠A=∠ABD;④AB•BC=AC•BD.其中单独能够判定△ABD∽△ACB的个数是( )
如图,在△ABC中,D是边AC上一点,连接BD,给出下列条件:①∠ABD=∠ACB;②AB2=AD•AC;③∠A=∠ABD;④AB•BC=AC•BD.其中单独能够判定△ABD∽△ACB的个数是( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
15.下面四组图形中,必是相似三角形的为( )
| A. | 有一个角为40°的两个等腰三角形 | |
| B. | 两个直角三角形 | |
| C. | 两条边对应成比例,一个对应角相等的两个三角形 | |
| D. | 有一个角为100°的两个等腰三角形 |