题目内容
2.二次函数y=ax2+bx+c(a,b,c为常数,a<0)的图象经过点(-1,1),(4,-4).下列结论:①$\frac{a}{c}$<0;
②当x>1时,y的值随x值的增大而减小;
③x=4是方程ax2+(b+1)x+c=0的一个根;
④当-1<x<4时,ax2+(b+1)x+c>0.
其中正确的是( )
| A. | ①③ | B. | ①②④ | C. | ①③④ | D. | ②③④ |
分析 ①将(-1,1)、(4,-4)分别代入y=ax2+bx+c,即可得出4a=-c,从而得出$\frac{a}{c}$<0,
②不能得出对称轴方程,所以当x>1时,y的值随x值的增大而减小不一定正确;
③把x=4代入方程ax2+(b+1)x+c=0整理得,16a+4b+c=-4,把(4,-4)代入y=ax2+bx+c得,16a+4b+c=-4,从而判定x=4是方程ax2+(b+1)x+c=0的一个根;
④由题意可知,当-1<x<4时,函数y=ax2+bx+c的图象在直线y=-x的上方,所以ax2+bx+c>-x,从而得出ax2+(b+1)x+c>0.
解答 解:∵二次函数y=ax2+bx+c的图象经过(-1,1),(4,-4).
∴$\left\{\begin{array}{l}{a-b+c=1①}\\{16a+4b+c=-4②}\end{array}\right.$,
②+①×4,整理,得4a=-c,
∴$\frac{a}{c}$=-$\frac{1}{4}$<0,故①正确;
∵不能得出对称轴方程,所以当x>1时,y的值随x值的增大而减小不一定正确;故②错误;
把x=4代入方程ax2+(b+1)x+c=0整理得,16a+4b+c=-4,
把(4,-4)代入y=ax2+bx+c得,16a+4b+c=-4,
∴x=4是方程ax2+(b+1)x+c=0的一个根,故③正确;
由题意可知,当-1<x<4时,函数y=ax2+bx+c的图象在直线y=-x的上方,
∴ax2+bx+c>-x,
∴ax2+(b+1)x+c>0,故④正确.
故选C.
点评 本题考查了二次函数y=ax2+bx+c的图象与系数的关系:当a<0,抛物线开口向下;抛物线的对称轴为直线x=-$\frac{b}{2a}$;抛物线与y轴的交点坐标为(0,c);当b2-4ac>0,抛物线与x轴有两个交点.

 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案| A. | (3,-1) | B. | (-3,1) | C. | (-3,-1) | D. | (3,1) |
| A. | 10 | B. | 8 | C. | 8或10 | D. | 不能确定 |
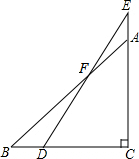 在△ABC中,∠C=90°,∠B=55°点D在边BC上,点E在CN的延长线上,连接DE,∠E=25°,求∠BFD的度数.
在△ABC中,∠C=90°,∠B=55°点D在边BC上,点E在CN的延长线上,连接DE,∠E=25°,求∠BFD的度数.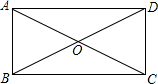 如图,在矩形ABCD中,对角线AC、BD相交于点O,∠AOB=60°,AB=5,则AD的长是5$\sqrt{3}$.
如图,在矩形ABCD中,对角线AC、BD相交于点O,∠AOB=60°,AB=5,则AD的长是5$\sqrt{3}$. 一辆货车从百货商店出发,向东走4.5千米到达王颖家,然后向西走1.5千米到达李明家.又向西走8千米达到周斌家,最后回到百货商店.
一辆货车从百货商店出发,向东走4.5千米到达王颖家,然后向西走1.5千米到达李明家.又向西走8千米达到周斌家,最后回到百货商店.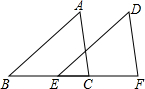 已知:如图,点B、E、C、F在同一条直线上,且AB=DE,AC=DF,BE=CF.求证:AB∥DE.请将下面的过程和理由补充完整
已知:如图,点B、E、C、F在同一条直线上,且AB=DE,AC=DF,BE=CF.求证:AB∥DE.请将下面的过程和理由补充完整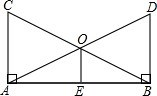 如图,∠BAC=∠ABD=90°,AC=BD,点O是AD,BC的交点,点E是AB的中点.试判断OE和AB的位置关系,并说明理由.
如图,∠BAC=∠ABD=90°,AC=BD,点O是AD,BC的交点,点E是AB的中点.试判断OE和AB的位置关系,并说明理由.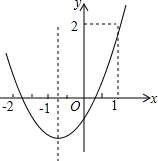 二次函数y=ax2+bx+c的图象如图所示,则下列说法:①abc<0;②2a>b;③a+c>1;④9a+c<3b+2,其中正确的个数是( )
二次函数y=ax2+bx+c的图象如图所示,则下列说法:①abc<0;②2a>b;③a+c>1;④9a+c<3b+2,其中正确的个数是( )