题目内容
16.解方程.(1)x2+4x-5=0(用配方法)
(2)2x2-7x+1=0(用公式法)
(3)(x+2)2-25=0
(4)x(x-2)+x-2=0.
分析 (1)利用配方法得到(x+2)2=9,然后利用直接开平方法解方程;
(2)先计算判别式的值,然后利用求根公式法解方程;
(3)利用因式分解法解方程;
(4)利用因式分解法解方程.
解答 解:(1)x2+4x=5,
x2+4x+4=9,
(x+2)2=9,
x+2=±3,
所以x1=1,x2=-5;
(2)△=(-7)2-4×2×1=41,
x=$\frac{7±\sqrt{41}}{2×2}$
所以x1=$\frac{7+\sqrt{41}}{4}$,x2=$\frac{7-\sqrt{41}}{4}$;
(3)(x+2-5)(x+2+5)=0,
x+2-5=0或x+2+5=0,
所以x1=3,x2=-7;
(4)(x-2)(x+1)=0,
x-2=0或x+1=0,
所以x1=2,x2=-1.
点评 本题考查了解一元二次方程-因式分解法:先把方程的右边化为0,再把左边通过因式分解化为两个一次因式的积的形式,那么这两个因式的值就都有可能为0,这就能得到两个一元一次方程的解,这样也就把原方程进行了降次,把解一元二次方程转化为解一元一次方程的问题了(数学转化思想).也考查了配方法和公式法解一元二次方程.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
6.如图,按图中结构规律的第20个图形中三角形的个数是( )

| A. | 75个 | B. | 77个 | C. | 79 个 | D. | 81个 |
11.已知一元二次方程x2-6x+8=0的两个根是等腰三角形的底和腰,则这个三角形的周长是( )
| A. | 10 | B. | 8 | C. | 8或10 | D. | 不能确定 |
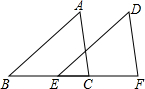 已知:如图,点B、E、C、F在同一条直线上,且AB=DE,AC=DF,BE=CF.求证:AB∥DE.请将下面的过程和理由补充完整
已知:如图,点B、E、C、F在同一条直线上,且AB=DE,AC=DF,BE=CF.求证:AB∥DE.请将下面的过程和理由补充完整 如图,已知AO=DO,CO=BO,求证:△AOC≌△DOB.
如图,已知AO=DO,CO=BO,求证:△AOC≌△DOB.