题目内容
18.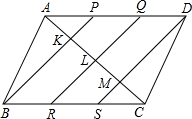 如图,在?ABCD中,P,Q是AD边上的三等分点,R,S是BC边上的三等分点,K,L,M分别是PB,QR,DS与对角线AC的交点.求证:AK=KL=LM=MC.
如图,在?ABCD中,P,Q是AD边上的三等分点,R,S是BC边上的三等分点,K,L,M分别是PB,QR,DS与对角线AC的交点.求证:AK=KL=LM=MC.
分析 根据平行四边形的性质得到AD=BC,AD∥BC,根据题意证明四边形PBRQ是平行四边形,得到PB∥QR,根据平行线分线段成比例定理证明结论.
解答 证明:∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,
∵P,Q是AD边上的三等分点,
∴AP=PQ=QC=$\frac{1}{3}$AD,
∵R,S是BC边上的三等分点,
∴BR=RS=SC=$\frac{1}{3}$BC,
∴PQ=BR,又AD∥BC,
∴四边形PBRQ是平行四边形,
∴PB∥QR,
同理DS∥QR,
∴PB∥QR∥DS,又AP=PQ=QC,BR=RS=SC,
∴AK=KL=LM=MC.
点评 本题考查的是平行线分线段成比例定理,灵活运用定理、找准对应关系是解题的关键,注意平行四边形的性质的正确运用.

练习册系列答案
相关题目
6.已知a=$\sqrt{2}$,b=$\sqrt{5}$,则$\frac{{a}^{2}-{b}^{2}}{{a}^{2}-ab}÷\frac{1}{a}$的值为( )
| A. | $\sqrt{5}-\sqrt{2}$ | B. | 3 | C. | $\sqrt{2}+\sqrt{5}$ | D. | $\sqrt{2}-\sqrt{5}$ |
12.计算:(-5)×(-4)×(-6)×(-5)的结果是( )
| A. | 600 | B. | -600 | C. | 20 | D. | -20 |
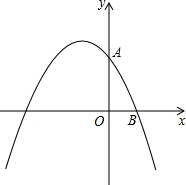 如图,已知点A(0,4)和点B(3,0)都在抛物线y=mx2+2mx+n上.
如图,已知点A(0,4)和点B(3,0)都在抛物线y=mx2+2mx+n上.