题目内容
7.在△ABC中,∠ABC=90°,AC=BC,直线l经过点C,AD⊥l,BE⊥l,垂足分别为D、E,直线l绕点C旋转时,DE、AD、BE具有怎样的数量关系?说出你的猜想,并证明.分析 画出如图1、2、3,分三种情况:
(1)DE=AD+BE,首先证明△ACD≌△CBE,可得AD=CE,CD=BE,进而得到DE=CE+CD=AD+BE;
(2)DE=AD-BE,首先证明△ADC≌△CEB,可得AD=CE,DC=BE,进而得到DE=AD-BE;
(3)与(2)类似,可证出DE=BE-AD
解答 解:(1)DE=AD+BE.
证明:∵∠DAC+∠ACD=90°,∠ACD+∠ECB=90°,
∴∠DAC=∠ECB,
在△DAC和△ECB中
$\left\{\begin{array}{l}{∠DAC=∠ECB}\\{∠ADC=∠CEB}\\{AC=BC}\end{array}\right.$,
∴△ACD≌△CBE(AAS),
∴AD=CE,CD=BE,
∴DE=CE+CD=AD+BE;
(2)DE=AD-BE;
∵∠ACB=90°,∠ADC=90°,
∴∠2+∠3=90°,∠1+∠3=90°,
∴∠1=∠2,
在△ADC和△CEB中,
$\left\{\begin{array}{l}{∠1=∠2}\\{∠ADC=∠CEB}\\{AC=BC}\end{array}\right.$,
∴△ADC≌△CEB(AAS),
∴AD=CE,DC=BE,
∴DE=CE-CD=AD-BE;
(3)DE=BE-AD.
和(2)一样可证△ADC≌△CEB,
∴AD=CE,DC=BE,
∴DE=CD-CE=BE-AD.
点评 本题考查了旋转的性质:旋转前后两图形全等,对应点到旋转中心的距离相等,对应点与旋转中心的连线段所夹的角等于旋转角.也考查了直角三角形全等的判定与性质.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
7.一组数据4,3,6,9,6,5的极差和众数分别是( )
| A. | 5和5.5 | B. | 5.5和6 | C. | 5和6 | D. | 6和6 |
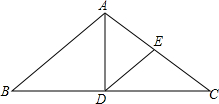 如图所示,已知:△ABC中,AB=AC,D是BC的中点,E是AC的中点,若∠EDC=∠C,BC=32cm,DE=10cm,求△ABC的面积.
如图所示,已知:△ABC中,AB=AC,D是BC的中点,E是AC的中点,若∠EDC=∠C,BC=32cm,DE=10cm,求△ABC的面积.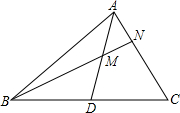 如图,若点M是△ABC的中线AD的中点,延长BM交AC于N,则AN:NC=1:2.
如图,若点M是△ABC的中线AD的中点,延长BM交AC于N,则AN:NC=1:2.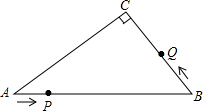 如图,在Rt△ABC中,∠C=90°,AB=10cm,AC:BC=4:3,点P从点A出发沿AB方向向点B运动,速度为1cm/s,同时点Q从点B出发沿B→C→A方向向点A运动,速度为2cm/s,当一个运动点到达终点时,另一个运动点也随之停止运动.
如图,在Rt△ABC中,∠C=90°,AB=10cm,AC:BC=4:3,点P从点A出发沿AB方向向点B运动,速度为1cm/s,同时点Q从点B出发沿B→C→A方向向点A运动,速度为2cm/s,当一个运动点到达终点时,另一个运动点也随之停止运动. 如图,直线l与⊙O相切于点C,A、B、D均在⊙O上,OA∥l,∠BDC=85°,则∠BAO的度数为50°.
如图,直线l与⊙O相切于点C,A、B、D均在⊙O上,OA∥l,∠BDC=85°,则∠BAO的度数为50°.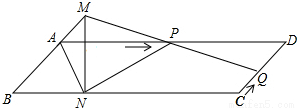 已知:如图,?ABCD中,AD=3cm,CD=1cm,∠B=45°,点P从点A出发,沿AD方向匀速运动,速度为3cm/s;点Q从点C出发,沿CD方向匀速运动,速度为1cm/s,连接并延长QP交BA的延长线于点M,过M作MN⊥BC,垂足是N,设运动时间为t(s)(0<t<1)
已知:如图,?ABCD中,AD=3cm,CD=1cm,∠B=45°,点P从点A出发,沿AD方向匀速运动,速度为3cm/s;点Q从点C出发,沿CD方向匀速运动,速度为1cm/s,连接并延长QP交BA的延长线于点M,过M作MN⊥BC,垂足是N,设运动时间为t(s)(0<t<1)