题目内容
9.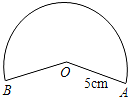 小明用图中所示的扇形纸片作一个圆锥的侧面,小明用图中所示的扇形纸片作一个圆锥的侧面,已知扇形的半径为5cm,弧长是6πcm,那么这个的圆锥的高是( )
小明用图中所示的扇形纸片作一个圆锥的侧面,小明用图中所示的扇形纸片作一个圆锥的侧面,已知扇形的半径为5cm,弧长是6πcm,那么这个的圆锥的高是( )| A. | 4cm | B. | 6cm | C. | 8cm | D. | 2cm |
分析 设圆锥底面圆的半径为r,根据圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长得到2πr=6π,解得r=3,然后利用勾股定理计算这个的圆锥的高.
解答 解:设圆锥底面圆的半径为r,
根据题意得2πr=6π,
解得r=3.
所以这个的圆锥的高=$\sqrt{{5}^{2}-{3}^{2}}$=4(cm).
故选A.
点评 本题考查了圆锥的计算:圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长.

练习册系列答案
相关题目
3.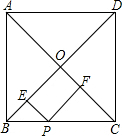 如图,在边长为1的正方形ABCD中,对角线AC和BD相交于点O,P是BC边上任意一点,PE⊥BD于点E,PF⊥AC于点F,则PE+PF=( )
如图,在边长为1的正方形ABCD中,对角线AC和BD相交于点O,P是BC边上任意一点,PE⊥BD于点E,PF⊥AC于点F,则PE+PF=( )
 如图,在边长为1的正方形ABCD中,对角线AC和BD相交于点O,P是BC边上任意一点,PE⊥BD于点E,PF⊥AC于点F,则PE+PF=( )
如图,在边长为1的正方形ABCD中,对角线AC和BD相交于点O,P是BC边上任意一点,PE⊥BD于点E,PF⊥AC于点F,则PE+PF=( )| A. | $\sqrt{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\sqrt{3}$ | D. | $\frac{\sqrt{3}}{2}$ |
19.要使代数式$\frac{1}{\sqrt{3x-1}}$有意义,则x的取值范围是( )
| A. | x>$\frac{1}{3}$ | B. | x<-$\frac{1}{3}$ | C. | x<$\frac{1}{3}$ | D. | x>-$\frac{1}{3}$ |
18.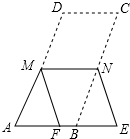 如图,在?ABCD中,∠A=70°,将?ABCD折叠,使点D、C分别落在点F、E处(点F、E都在AB所在的直线上),折痕为MN,则∠AMF等于( )
如图,在?ABCD中,∠A=70°,将?ABCD折叠,使点D、C分别落在点F、E处(点F、E都在AB所在的直线上),折痕为MN,则∠AMF等于( )
 如图,在?ABCD中,∠A=70°,将?ABCD折叠,使点D、C分别落在点F、E处(点F、E都在AB所在的直线上),折痕为MN,则∠AMF等于( )
如图,在?ABCD中,∠A=70°,将?ABCD折叠,使点D、C分别落在点F、E处(点F、E都在AB所在的直线上),折痕为MN,则∠AMF等于( )| A. | 70° | B. | 40° | C. | 30° | D. | 20° |
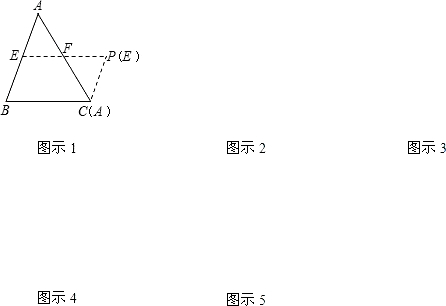
 如图,△ABC内接于⊙O,∠C=45°,AB=2,则⊙O的半径为$\sqrt{2}$.
如图,△ABC内接于⊙O,∠C=45°,AB=2,则⊙O的半径为$\sqrt{2}$.