题目内容
2.若关于x的一元二次方程2x2-x+m=0有两个不相等的实数根,则m的整数值可能是-1(写出一个即可).分析 根据一元二次方程的根的判别式,建立关于m的不等式,求出m的取值范围即可.
解答 解:∵关于x的一元二次方程x2+x-2+m=0有两个不相等的实数根,
∴△=b2-4ac=1-4×2m>0,
∴m<$\frac{1}{8}$.
∴m的取值范围是m<$\frac{1}{8}$;
∴m的整数值可能是-1,
故答案为:-1.
点评 此题考查了根的判别式,一元二次方程根的情况与判别式△的关系:(1)△>0?方程有两个不相等的实数根;(2)△=0?方程有两个相等的实数根;(3)△<0?方程没有实数根.

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案
相关题目
17.已知实数x=4,y=8,则以x,y的值为两边长的等腰三角形的周长是( )
| A. | 20 | B. | 16 | C. | 20或16 | D. | 以上答案均不对 |
12.下列方程中,关于x的一元二次方程是( )
| A. | ax2+bx+c=0 | B. | $\frac{1}{{x}^{2}}+\frac{1}{x}$-2=0 | C. | x2+2x-1=0 | D. | x2+2x=x2-1 |
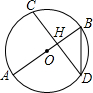 如图,弦CD垂直于⊙O的直径AB,垂足为H,且CD=2$\sqrt{2}$,BD=$\sqrt{3}$,则BH的长为( )
如图,弦CD垂直于⊙O的直径AB,垂足为H,且CD=2$\sqrt{2}$,BD=$\sqrt{3}$,则BH的长为( )