题目内容
12．
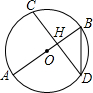如图，弦CD垂直于⊙O的直径AB，垂足为H，且CD=2$\sqrt{2}$，BD=$\sqrt{3}$，则BH的长为（ ）| A． | 2 | B． | 3 | C． | 4 | D． | 1 |
分析 首先连接OD，由弦CD垂直于⊙O的直径AB，垂足为H，根据垂径定理的即可求得OH的长，然后由勾股定理则可求得BH的长．
解答 
解：连接OD，
∵⊙O的直径AB，且AB⊥CD，
∴DH=$\frac{1}{2}$CD=$\frac{1}{2}$×2$\sqrt{2}$=$\sqrt{2}$，
∵BD=$\sqrt{3}$，
在Rt△BDH中，BH=$\sqrt{B{D}^{2}-D{H}^{2}}$=1，
故选D．
点评 本题考查的是垂径定理，根据题意作出辅助线，构造出直角三角形是解答此题的关键．
练习册系列答案
名师金手指领衔课时系列答案
相关题目
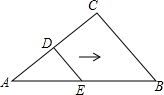如图，D、E分别是AC和AB上的点，AD=DC=4，DE=3，DE∥BC，∠C=90°，将△ADE沿着AB边向右平移，当点D落在BC上时，平移的距离为5．
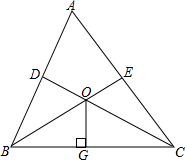如图，△ABC中，∠BAC=60°，点D、E分别在AB、AC上，∠BCD=∠CBE=30°，BE、CD相交于点O，OG⊥BC于点G，求证：OE+OD=2OG．
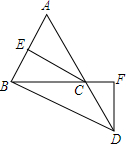如图，在△ABC中，延长AC至点D，使CD=BC，连接BD，作CE⊥AB于点E，DF⊥BC交BC的延长线于点F，且AB=AC．如果∠ABD=105°，∠A=40度．