��Ŀ����
3����ͼ����ABC�DZ߳�Ϊ2$\sqrt{3}$�ĵȱ������Σ���֪G�DZ�AB�ϵ�һ�����㣨G�㲻��A��B���غϣ�����GE��AC��GF��BC����AG=x��S��GEF=y��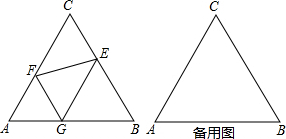
��1����y��x�ĺ�����ϵʽ����д������������
��2����G���˶������ܣ��ܷ�ʹ��GEF��Ϊֱ�������Σ����ܣ������AG���ȣ������ܣ���˵�����ɣ�
��3����G���˶������У��ܷ�ʹ�ı���GFEB����ƽ���ı��Σ����ܣ�ֱ��д��S��GEF��ֵ�������ܣ���˵�����ɣ�
���� ��1�������⣬�ã���AFG����BEGΪ�ȱ������Σ�������FG=AG=x��EG=BG=2$\sqrt{3}$-x����EGF=60�㣬�������ε�����������ɵõ�y��x�ĺ�����ϵʽ��
��2���ɣ�1��֪��EGF=60�㣬��������ۣ���EFG=90�㣬��FEG=90�㣬����������ɺ�30���ֱ�������ε����ʼ���������ۣ�
��3�����ı���GFEB����ƽ���ı���ʱ����֤��AFG����BEG����CEF����EFG��ȫ�ȵĵȱ������Σ�����S��GEF��
���  �⣺��1���ߡ�ABC�ǵȱ������Σ�GF��BC��
�⣺��1���ߡ�ABC�ǵȱ������Σ�GF��BC��
���AGF=��B=60�㣬
���AFG�ǵȱ������Σ�
ͬ����BEGΪ�ȱ������Σ�
��FG=AG=x��EG=BG=2$\sqrt{3}$-x����EGF=60�㣬
y=$\frac{1}{2}x��2\sqrt{3}-x��sin60��$=-$\frac{\sqrt{3}}{4}{x}^{2}+\frac{3}{2}x$��������0��2$\sqrt{3}$����
��2������EFG=90�㣬�֡�EGF=60�㣬���ԣ���x=$\frac{1}{2}$��2$\sqrt{3}$-x������ã�x=$\frac{2\sqrt{3}}{3}$��
����FEG=90�㣬��$\frac{1}{2}x=2\sqrt{3}-x$����ã�x=$\frac{4\sqrt{3}}{3}$��
���ԣ���ʹ��GEF��Ϊֱ�������Σ�AG�ij�Ϊ$\frac{2\sqrt{3}}{3}$��$\frac{4\sqrt{3}}{3}$��
��3�����ı���GFEB����ƽ���ı���ʱ��
�ɣ�1����AFG�͡�BEGΪ�ȱ������Σ�
���CEG�ǵȱ������Σ�
���EFG=��FEG=60�㣬
���EFGΪ�ȱ������Σ�
��EF=FG=AG=GB=$\frac{1}{2}AB$=$\sqrt{3}$��
��SAGEF=$\frac{1}{2}FG•EGsin60��$=$\frac{1}{2}��\sqrt{3}��\sqrt{3}��\frac{\sqrt{3}}{2}$=$\frac{3\sqrt{3}}{4}$��
���� ������Ҫ�����˵ȱ������ε��ж������ʣ������ε����������ƽ���ı��ε����ʣ���30���ֱ�������ε����ʣ������Ӧ����Щ�����ǽ���Ĺؼ���ͬʱע�����˼���Ӧ�ã�

| A�� | 0 | B�� | -2 | C�� | �� | D�� | -1 |
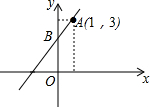 ��ͼ��ֱ��y=kx+b����A��1��3����B��0��2���������x�IJ���ʽkx+b��3�Ľ⼯�ǣ�������
��ͼ��ֱ��y=kx+b����A��1��3����B��0��2���������x�IJ���ʽkx+b��3�Ľ⼯�ǣ�������| A�� | x��1 | B�� | x��1 | C�� | x��0 | D�� | x��0 |
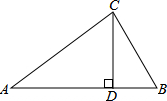 ��ͼ��CD��Rt��ABCб��AB�ϵĸߣ�CD=6��BD=4����AB�ij�Ϊ��������
��ͼ��CD��Rt��ABCб��AB�ϵĸߣ�CD=6��BD=4����AB�ij�Ϊ��������| A�� | 10 | B�� | 11 | C�� | 12 | D�� | 13 |
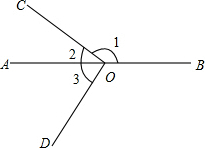 ��ͼ����֪��O��ֱ��AB�ϣ�CO��DO������1=155�㣬���3�Ķ���Ϊ��������
��ͼ����֪��O��ֱ��AB�ϣ�CO��DO������1=155�㣬���3�Ķ���Ϊ��������| A�� | 35�� | B�� | 45�� | C�� | 55�� | D�� | 65�� |
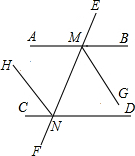 ��ͼ����֪AB��CD��MG��NH�ֱ�ƽ�֡�BMN���CNM����˵��NH��MG��
��ͼ����֪AB��CD��MG��NH�ֱ�ƽ�֡�BMN���CNM����˵��NH��MG��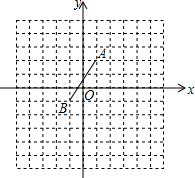 ��ͼ����ƽ��ֱ������ϵ�У���֪����A��1��2����B��-1��-1����
��ͼ����ƽ��ֱ������ϵ�У���֪����A��1��2����B��-1��-1����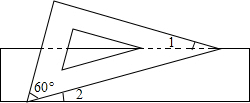 ��ͼ����һ�麬��60��ǵ�ֱ�����ǰ������������ڳ����εĶԱ��ϣ������1=16�㣬��ô��2�Ķ�����14�㣮
��ͼ����һ�麬��60��ǵ�ֱ�����ǰ������������ڳ����εĶԱ��ϣ������1=16�㣬��ô��2�Ķ�����14�㣮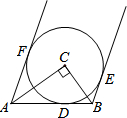 ��ͼ����Rt��ABC�У���C=90�㣬�Ե�CΪԲ������C����AB���ڵ�D������A��B�ֱ�����C������AF��BE���е�ΪF��E�㣮��֤��AF��BE��
��ͼ����Rt��ABC�У���C=90�㣬�Ե�CΪԲ������C����AB���ڵ�D������A��B�ֱ�����C������AF��BE���е�ΪF��E�㣮��֤��AF��BE��