题目内容
14.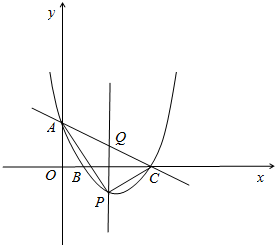 如图,在平面直角坐标系中,抛物线y=$\frac{4}{5}$x2-$\frac{24}{5}$x+4交y轴于点A,交x轴于B、C两点且B在C左边.设点P是直线AC下方抛物线上的点(不与A、C重合),过P作PQ∥y轴交线段AC于Q,若点P的横坐标为x,连接PA、PC.
如图,在平面直角坐标系中,抛物线y=$\frac{4}{5}$x2-$\frac{24}{5}$x+4交y轴于点A,交x轴于B、C两点且B在C左边.设点P是直线AC下方抛物线上的点(不与A、C重合),过P作PQ∥y轴交线段AC于Q,若点P的横坐标为x,连接PA、PC.(1)用x的代数式表示线段PQ的长;
(2)设△PAC的面积为S,求S与x之间的函数关系式.
分析 (1)先根据抛物线的解析式求出A、B、C的坐标,然后根据待定系数法求得直线AC的解析式,根据题意若点P的横坐标为x,则P(x,$\frac{4}{5}$x2-$\frac{24}{5}$x+4),Q(x,-$\frac{4}{5}$x+4),进而即可求得线段PD;
(2)S=S△APQ+S△PQC=$\frac{1}{2}$PQ•OC即可求得.
解答 解:(1)∵抛物线y=$\frac{4}{5}$x2-$\frac{24}{5}$x+4交y轴于点A,交x轴于B、C两点且B在C左边.
∴令x=0,y=4,令y=0,则$\frac{4}{5}$x2-$\frac{24}{5}$x+4=0,解得x1=1,x2=5,
∴A(0,4),B(1,0),C(5,0),
设直线AC的解析式为y=kx+b,则$\left\{\begin{array}{l}{b=4}\\{5k+b=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=-\frac{4}{5}}\\{b=4}\end{array}\right.$,
∴直线AC的解析式为y=-$\frac{4}{5}$x+4,
∵PQ∥y轴交线段AC于Q,若点P的横坐标为x,
∴P(x,$\frac{4}{5}$x2-$\frac{24}{5}$x+4),Q(x,-$\frac{4}{5}$x+4),
∴PQ=(-$\frac{4}{5}$x+4)-($\frac{4}{5}$x2-$\frac{24}{5}$x+4)=-$\frac{4}{5}$x2+4x;
(2)∵S=S△APQ+S△PQC=$\frac{1}{2}$PQ•OC,
∴S=$\frac{1}{2}$(-$\frac{4}{5}$x2+4x)×5=-2x2+10x(0<x<5).
点评 本题考查了直线和抛物线的交点,待定系数法求直线的解析式和抛物线的解析式以及三角形面积等,求得P、Q点的坐标是解题的关键.

| A. | 一组 | B. | 三组 | C. | 四组 | D. | 无数组 |
 已知,如图,在△ABC中,AD平分∠BAC,E是CA延长线上的一点,EG∥AD,交AB于F,求证:AE=AF.
已知,如图,在△ABC中,AD平分∠BAC,E是CA延长线上的一点,EG∥AD,交AB于F,求证:AE=AF.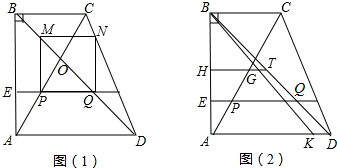
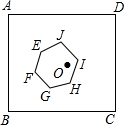 如图,正方形ABCD的边长为1,中心为点O,有一边长大小不定的正六边形EFGHIJ绕点O可任意旋转,在旋转过程中,这个正六边形始终在正方形ABCD内(包括正方形的边),当这个正六边形的边长最大时,AE的最小值为$\frac{\sqrt{2}-1}{2}$.
如图,正方形ABCD的边长为1,中心为点O,有一边长大小不定的正六边形EFGHIJ绕点O可任意旋转,在旋转过程中,这个正六边形始终在正方形ABCD内(包括正方形的边),当这个正六边形的边长最大时,AE的最小值为$\frac{\sqrt{2}-1}{2}$.