Question

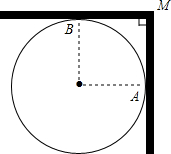小红家的锅盖坏了，为了配一个锅盖，需要测量锅的直径（锅沿所形成的圆的直径），而小红家只有一把长20cm的直尺，根本不够长，怎么办呢？小红想了想，采取了以下办法：如图，首先把锅平放到墙根，锅沿刚好靠到两墙，用直尺紧贴墙面量得MA的长，即可求出锅的直径．请你利用图说明她这样做的理由．

Answer 1

考点：切线的性质

专题：应用题

分析：要求直径，可先求锅沿所形成圆的半径，连OA、OB，则可得正方形OAMB，于是找到了和OA有关系的线段MA了，只要测量MA，就可知直径．

解答：解：假设圆（锅沿所形成的圆）的圆心为O，连接OA，OB．
∵MA，MB与⊙O相切，
∴∠OAM=∠OBM=90°；
又∵∠M=90°，
∴四边形OAMB是矩形，
∵OA=OB，
∴四边形OAMB是正方形．
∴OA=MA，
∴量得MA的长，
再乘以2就是锅的直径．

点评：此题是一道开放性试题，考查的是切线性质的实际应用，运用切线的性质可证明四边形OAMB为正方形，于是可求锅的直径．