题目内容
7.解方程:(1)$\frac{2-x}{3+x}$=$\frac{1}{2}$+$\frac{1}{x+3}$
(2)$\frac{5m-4}{2m-4}$=$\frac{2m+5}{3m-6}$-1.
分析 (1)首先方程的两边同乘以最简公分母2(x+3),把分式方程转化为整式方程,再求解即可,最后要把求得的x的值代入到最简公分母进行检验.
(2)首先方程的两边同乘以最简公分母6(m-2),把分式方程转化为整式方程,再求解即可,最后要把求得的m的值代入到最简公分母进行检验.
解答 解:(1)$\frac{2-x}{3+x}$=$\frac{1}{2}$+$\frac{1}{x+3}$,
方程两边同乘以最简公分母2(x+3)得:
2(2-x)=x+3+2,
解得:x=-$\frac{1}{3}$,
检验:把x=-$\frac{1}{3}$代入2(x+3)得:2×(-$\frac{1}{3}$+3)≠0,
故原方程的解为x=-$\frac{1}{3}$.
(2)$\frac{5m-4}{2m-2}$=$\frac{2m+5}{3m-6}$-1,
方程两边同乘以最简公分母6(m-2)得:
3(5m-4)=2(2m+5)-6(m-2),
解得:m=2,
检验:把m=2代入6(m-2)得:6×(2-2)=0,
故原方程无解.
点评 本题主要考查解分式方程,关键在于“转化思想”,把分式方程转化为整式方程求解,最后一定注意要验根.

练习册系列答案
相关题目
15.下列分式为最简分式的是( )
| A. | $\frac{3b}{15a}$ | B. | $\frac{{a}^{2}-{b}^{2}}{a-b}$ | C. | $\frac{{x}^{2}}{3x}$ | D. | $\frac{{x}^{2}+y2}{x+y}$ |
 如图,抛物线y=-ax2+bx+5过点(1,2)、(4,5),交y轴于点B,直线
如图,抛物线y=-ax2+bx+5过点(1,2)、(4,5),交y轴于点B,直线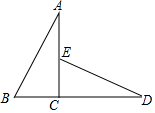 如图,△ABC≌△DEC且∠AED=120°,B,C,D三点在一条直线上,CD=2$\sqrt{3}$cm,AB=4cm,则∠D=30°;AE=(2$\sqrt{3}$-2)cm.
如图,△ABC≌△DEC且∠AED=120°,B,C,D三点在一条直线上,CD=2$\sqrt{3}$cm,AB=4cm,则∠D=30°;AE=(2$\sqrt{3}$-2)cm.