题目内容
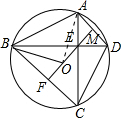
 如图,在⊙O中,AD∥BC,AC⊥BD垂足为E.
如图,在⊙O中,AD∥BC,AC⊥BD垂足为E.(1)求证:BE=CE;
(2)若AD=4,M为AD的中点,延长ME交BC于F,
①判断EF与BC的位置关系;
②求OF的长度.
考点:全等三角形的判定与性质,线段垂直平分线的性质,圆周角定理
专题:
分析:(1)易证∠CBE=∠CAD和∠CAD=∠ECB,即可求得∠CBE=∠ECB,即可解题;
(2)①易证AE=DE,根据M为AD的中点和等腰三角形底边三线合一的性质,可得∠EFC=∠AMD=90°,根据(1)中结论BE=CE即可解题;
②连接AO,易证∠AOB=90°,即可求得∠AOM=∠OBF,即可证明△BOF≌△OAM,可得OF=AM,即可解题.
(2)①易证AE=DE,根据M为AD的中点和等腰三角形底边三线合一的性质,可得∠EFC=∠AMD=90°,根据(1)中结论BE=CE即可解题;
②连接AO,易证∠AOB=90°,即可求得∠AOM=∠OBF,即可证明△BOF≌△OAM,可得OF=AM,即可解题.
解答:(1)∵
=
,
∴∠CBE=∠CAD,
∵AD∥BC,
∴∠CAD=∠ECB,
∴∠CBE=∠ECB,
∴BE=CE;
(2)①EF垂直平分BC;
理由:∵AD∥BC,
∴∠CBE=∠ADE,
∵∠CBE=∠CAD,
∴∠ADE=∠CAD,
∴AE=DE,
∵M为AD的中点,
∴EM⊥AD,
∴∠AME=90°,
∵AD∥BC,
∴∠EFC=∠AMD=90°,
∴EF⊥BC,
∵BE=CE,
∴BF=FC,
∴EF垂直平分BC;
②连接AO,
∵OB=OC,
∴O在BC的垂直平分线上,
∴O在EF上;
∵AC⊥BD,
∴∠BEC=90°,
∵BE=CE,
∴∠EBC=∠ECB=45°,
∴∠BOA=90°,
∵∠AOM+∠BOF=90°,∠BOF+∠OBF=90°,
∴∠AOM=∠OBF,
∵MF⊥BC,
∴∠MFC=90°,
∵AD∥BC,
∴∠AME=90°,
在△BOF和△OAM中,
,
∴△BOF≌△OAM,(AAS)
∴OF=AM=2.
 |
| CD |
 |
| CD |
∴∠CBE=∠CAD,
∵AD∥BC,
∴∠CAD=∠ECB,
∴∠CBE=∠ECB,
∴BE=CE;
(2)①EF垂直平分BC;
理由:∵AD∥BC,
∴∠CBE=∠ADE,
∵∠CBE=∠CAD,
∴∠ADE=∠CAD,
∴AE=DE,
∵M为AD的中点,
∴EM⊥AD,
∴∠AME=90°,
∵AD∥BC,
∴∠EFC=∠AMD=90°,
∴EF⊥BC,
∵BE=CE,
∴BF=FC,
∴EF垂直平分BC;
②连接AO,

∵OB=OC,
∴O在BC的垂直平分线上,
∴O在EF上;
∵AC⊥BD,
∴∠BEC=90°,
∵BE=CE,
∴∠EBC=∠ECB=45°,
∴∠BOA=90°,
∵∠AOM+∠BOF=90°,∠BOF+∠OBF=90°,
∴∠AOM=∠OBF,
∵MF⊥BC,
∴∠MFC=90°,
∵AD∥BC,
∴∠AME=90°,
在△BOF和△OAM中,
|
∴△BOF≌△OAM,(AAS)
∴OF=AM=2.
点评:本题考查了全等三角形的判定,考查了全等三角形对应边相等的性质,本题中求证△BOF≌△OAM是解题的关键.

练习册系列答案
相关题目
点P(-2,-1)关于y轴对称的点的坐标是( )
| A、(-2,-1) |
| B、(1,-2) |
| C、(2,-1) |
| D、(-1,-2) |
 如图,已知,在△ABC中,CD交AB于点E,AE:EB=1:3,EF∥BC∥AD,EF交AC于点F,S△ADE=a.求S△BCE和S△AEF的值.
如图,已知,在△ABC中,CD交AB于点E,AE:EB=1:3,EF∥BC∥AD,EF交AC于点F,S△ADE=a.求S△BCE和S△AEF的值. 已知二次函数y=ax2+bx+c的图象如图所示,其对称轴为直线x=-1,给出下列结论:(1)b2>4ac; (2)abc>0;(3)2a+b=0;(4)a+b+c>0;(5)a-b+c<0.其中正确的结论有( )
已知二次函数y=ax2+bx+c的图象如图所示,其对称轴为直线x=-1,给出下列结论:(1)b2>4ac; (2)abc>0;(3)2a+b=0;(4)a+b+c>0;(5)a-b+c<0.其中正确的结论有( )