题目内容
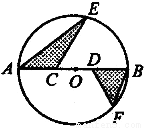
(6分)如图,在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O与AB边交于点D,过点D的切线,交BC于点E.
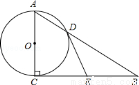
(1)求证:EB=EC;
(2)若以点O、D、E、C为顶点的四边形是正方形,试判断△ABC的形状,并说明理由.
【解析】
试题分析:(1)连接OD,根据圆周角定理得出∠ACB=90°,再由BC是⊙O的切线得出∠BCA=90°,由DE是⊙O的切线,得出ED=EC,∠ODE=90°,故可得出∠EDB=∠EBD,由此可得出结论.
(2)当以点O、D、E、C为顶点的四边形是正方形时,则△DEB是等腰直角三角形,据此即可判断.
试题解析:(1)证明:连接OD,
∵AC是直径,∠ACB=90°,
∴BC是⊙O的切线,∠BCA=90°.
又∵DE是⊙O的切线,
∴ED=EC,∠ODE=90°,
∴∠ODA+∠EDB=90°,
∵OA=OD,
∴∠OAD=∠ODA,
又∵∠OAD+∠DBE=90°,
∴∠EDB=∠EBD,
∴ED=EB,
∴EB=EC.

(2)【解析】
当以点O、D、E、C为顶点的四边形是正方形时,则∠DEB=90°,
又∵DE=BE,∴△DEB是等腰直角三角形,则∠B=45°,
∴△ABC是等腰直角三角形.
考点:切线的性质;等腰三角形的判定;正方形的性质.

练习册系列答案
相关题目

 个边长为1的正方形并排组成矩形OABC,相邻两边OA和OC分别落在x轴和y轴的正半轴上,设抛物线y=ax 2+bx+c(a<0)过矩形顶点B、C。
个边长为1的正方形并排组成矩形OABC,相邻两边OA和OC分别落在x轴和y轴的正半轴上,设抛物线y=ax 2+bx+c(a<0)过矩形顶点B、C。

 经过点A和C.
经过点A和C.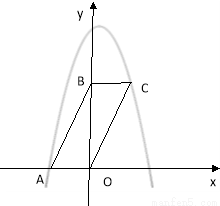
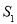 ,右侧部分图形的面积记为
,右侧部分图形的面积记为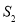 ,求
,求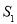 与
与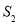 的比.
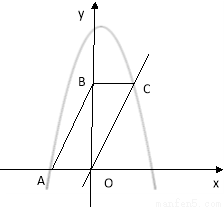
的比. ),将直线OC沿x轴平移到
),将直线OC沿x轴平移到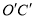 ,点D关于直线
,点D关于直线 的对称点记为
的对称点记为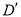 ,当点
,当点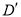 正好在抛物线上时,求出此时点
正好在抛物线上时,求出此时点 坐标并直接写出直线
坐标并直接写出直线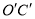 的函数解析式.
的函数解析式.

 米 C.
米 C. 米 D.50米
米 D.50米