题目内容
如图,在半径为2的扇形OAB中,∠AOB=90°,点C是弧AB上的—个动点(不与A,B重合),OD⊥BC,OE⊥AC,垂足分别为D,E,则DE的长度( )

A.1 B.2 C. D.
D.
C.
【解析】
试题分析:连接AB,由OD垂直于BC,OE垂直于AC,利用垂径定理得到D、E分别为BC、AC的中点,即ED为三角形ABC的中位线,由OA=OB=2,且∠AOB=90°,利用勾股定理求出AB的长,即可求出ED的长.
试题解析:连接AB,

∵OD⊥BC,OE⊥AC,
∴D、E分别为BC、AC的中点,
∴DE为△ABC的中位线,
∵OA=OB=2,∠AOB=90°,
∴根据勾股定理得:AB= ,
,
则DE= AB=
AB= .
.
故选C.
考点:1.垂径定理;2.三角形中位线定理.

练习册系列答案
 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目
 的值为5,则代数式
的值为5,则代数式 的值是 ( )
的值是 ( )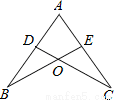
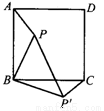
 个边长为1的正方形并排组成矩形OABC,相邻两边OA和OC分别落在x轴和y轴的正半轴上,设抛物线y=ax 2+bx+c(a<0)过矩形顶点B、C。
个边长为1的正方形并排组成矩形OABC,相邻两边OA和OC分别落在x轴和y轴的正半轴上,设抛物线y=ax 2+bx+c(a<0)过矩形顶点B、C。
 经过点A和C.
经过点A和C.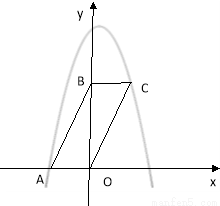
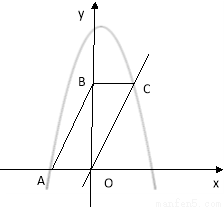
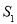 ,右侧部分图形的面积记为
,右侧部分图形的面积记为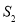 ,求
,求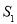 与
与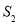 的比.
的比. ),将直线OC沿x轴平移到
),将直线OC沿x轴平移到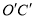 ,点D关于直线
,点D关于直线 的对称点记为
的对称点记为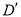 ,当点
,当点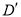 正好在抛物线上时,求出此时点
正好在抛物线上时,求出此时点 坐标并直接写出直线
坐标并直接写出直线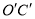 的函数解析式.
的函数解析式. (k≠0)的图象经过点(2,﹣1),则k的值为 .
(k≠0)的图象经过点(2,﹣1),则k的值为 .