题目内容
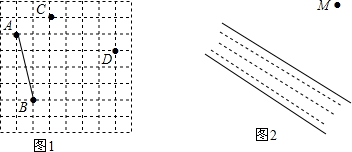
12．
如图，BD是菱形ABCD的对角线，CE⊥AB交于点E，交BD于点F，且点E是AB中点，则tan∠BFE的值是（ ）| A． | $\frac{1}{2}$ | B． | 2 | C． | $\frac{\sqrt{3}}{3}$ | D． | $\sqrt{3}$ |
分析 首先利用菱形的性质得出AB=BC，即可得出∠ABC=60°，再利用三角函数得出答案．
解答 解：∵四边形ABCD是菱形，
∴AB=BC，
∵CE⊥AB，点E是AB中点，
∴∠ABC=60°，
∴∠EBF=30°，
∴∠BFE=60°，
∴tan∠BFE的值为$\sqrt{3}$．
故选D．
点评 此题考查菱形的性质，关键是根据含30°的直角三角形的性质和三角函数解答．
练习册系列答案
轻松暑假总复习系列答案
相关题目
如图，点A，B，C在⊙O上，CO的延长线交AB于点D，∠A=50°，∠B=30°，则∠ADC的度数为110°．
7．甲、乙两人在100米直道AB上练习匀速往返跑，若甲、乙分别在A，B两端同时出发，分别到另一端点处掉头，掉头时间不计，速度分别为5m/s和4m/s．
（1）在坐标系中，虚线表示乙离A端的距离s（单位：m）与运动时间t（单位：s）之间的函数图象（0≤t≤200），请在同一坐标系中用实线画出甲离A端的距离s与运动时间t之间的函数图象（0≤t≤200）．
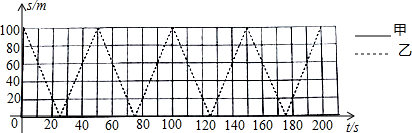
（2）根据（1）中所画图象，完成下列表格：
（3）①直接写出甲、乙两人分别在第一个100m内，t与s的函数解析式，并指出自变量t的取值范围．
②求甲、乙第6次相遇时t的值．
（1）在坐标系中，虚线表示乙离A端的距离s（单位：m）与运动时间t（单位：s）之间的函数图象（0≤t≤200），请在同一坐标系中用实线画出甲离A端的距离s与运动时间t之间的函数图象（0≤t≤200）．
（2）根据（1）中所画图象，完成下列表格：
| 两人相遇次数（单位：次） | 1 | 2 | 3 | 4 | … | n |
| 两人所跑路程之和（单位：m） | 100 | 300 | 500 | 700 | … | 200n-100 |
②求甲、乙第6次相遇时t的值．
4．2015年我国大学生毕业人数将达到7 490 000人，这个数据用科学记数法表示为（ ）
| A． | 7.49×107 | B． | 7.49×106 | C． | 74.9×105 | D． | 0.749×107 |
1．
如图是某校参加各兴趣小组的学生人数分布扇形统计图，则参加人数最多的兴趣小组是（ ）
如图是某校参加各兴趣小组的学生人数分布扇形统计图，则参加人数最多的兴趣小组是（ ）| A． | 棋类 | B． | 书画 | C． | 球类 | D． | 演艺 |
