题目内容
3.“保护环境,人人有责”,为了了解某市的空气质量情况,某校环保兴趣小组,随机抽取了2014年内该市若干天的空气质量情况作为样本进行统计,绘制了如图所示的条形统计图和扇形统计图(部分信息未给出).请你根据图中提供的信息,解答下列问题:
(1)补全条形统计图;
(2)估计该市这一年(365天)空气质量达到“优”和“良”的总天数;
(3)计算随机选取这一年内某一天,空气质量是“优”的概率.
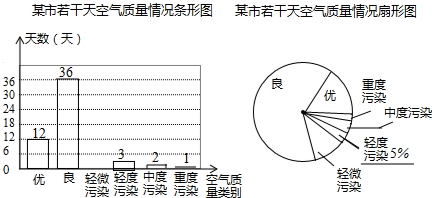
分析 (1)根据良的天数除以良的天数所占的百分比,可得样本容量,根据样本容量乘以轻微污染所占的百分比求出轻微污染的天数,可得答案;
(2)根据一年的时间乘以优良所占的百分比,可得答案;
(3)根据根据一年中优的天数比上一年的天数,可得答案.
解答  解:(1)样本容量3÷5%=60,
解:(1)样本容量3÷5%=60,
60-12-36-3-2-1=6,
条形统计图如图:
(2)这一年空气质量达到“优”和“良”的总天数为:
365×$\frac{36+12}{60}$=292;
(3)随机选取这一年内某一天,空气质量是“优”的概率为:$\frac{12}{60}$=$\frac{1}{5}$.
点评 本题考查的是条形图和扇形图以及用样本估计总体、概率的计算,从条形图和扇形图中获取正确的信息是解题的关键,注意概率公式的正确运用.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
14.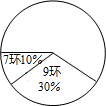 第17届亚洲运动会于2014年9月19日-10月4日在韩国仁川举行,中国射击队对这次仁川亚运会非常重视,在一次选拔赛中,运动员甲10次射击成绩的统计表和扇形统计图如下:
第17届亚洲运动会于2014年9月19日-10月4日在韩国仁川举行,中国射击队对这次仁川亚运会非常重视,在一次选拔赛中,运动员甲10次射击成绩的统计表和扇形统计图如下:
(1)求甲运动员几种7环和10环的次数,并补全扇形统计图;
(2)求甲运动员的10次设计的平均成绩是多少环;
(3)已知乙运动员10次射击的平均成绩为9环,方差为1.2,如果在这二人中选一人参加比赛,你认为应该派谁去?并说明理由.
 第17届亚洲运动会于2014年9月19日-10月4日在韩国仁川举行,中国射击队对这次仁川亚运会非常重视,在一次选拔赛中,运动员甲10次射击成绩的统计表和扇形统计图如下:
第17届亚洲运动会于2014年9月19日-10月4日在韩国仁川举行,中国射击队对这次仁川亚运会非常重视,在一次选拔赛中,运动员甲10次射击成绩的统计表和扇形统计图如下:| 命中环数 | 10 | 9 | 8 | 7 |
| 命中次数 | 4 | 3 | 2 | ,1 |
(2)求甲运动员的10次设计的平均成绩是多少环;
(3)已知乙运动员10次射击的平均成绩为9环,方差为1.2,如果在这二人中选一人参加比赛,你认为应该派谁去?并说明理由.
18. 如图是某几何体的三视图,根据图中所标的数据求得该几何体的体积为( )
如图是某几何体的三视图,根据图中所标的数据求得该几何体的体积为( )
 如图是某几何体的三视图,根据图中所标的数据求得该几何体的体积为( )
如图是某几何体的三视图,根据图中所标的数据求得该几何体的体积为( )| A. | 236π | B. | 136π | C. | 132π | D. | 120π |
15. 如图所示的几何体的左视图为( )
如图所示的几何体的左视图为( )
 如图所示的几何体的左视图为( )
如图所示的几何体的左视图为( )| A. |  | B. |  | C. |  | D. |  |
12. 如图,BD是菱形ABCD的对角线,CE⊥AB交于点E,交BD于点F,且点E是AB中点,则tan∠BFE的值是( )
如图,BD是菱形ABCD的对角线,CE⊥AB交于点E,交BD于点F,且点E是AB中点,则tan∠BFE的值是( )
 如图,BD是菱形ABCD的对角线,CE⊥AB交于点E,交BD于点F,且点E是AB中点,则tan∠BFE的值是( )
如图,BD是菱形ABCD的对角线,CE⊥AB交于点E,交BD于点F,且点E是AB中点,则tan∠BFE的值是( )| A. | $\frac{1}{2}$ | B. | 2 | C. | $\frac{\sqrt{3}}{3}$ | D. | $\sqrt{3}$ |
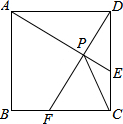 如图,在正方形ABCD中,动点E,F分别从D,C两点同时出发,以相同的速度在边DC,CB上移动,连接AE和DF交于点P,由于点E,F的移动,使得点P也随之运动.若AD=2,线段CP的最小值是$\sqrt{5}$-1.
如图,在正方形ABCD中,动点E,F分别从D,C两点同时出发,以相同的速度在边DC,CB上移动,连接AE和DF交于点P,由于点E,F的移动,使得点P也随之运动.若AD=2,线段CP的最小值是$\sqrt{5}$-1.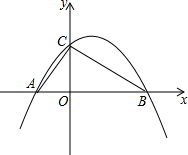 如图,已知抛物线y=ax2+bx+c经过A(-2,0),B(4,0),C(0,3)三点.
如图,已知抛物线y=ax2+bx+c经过A(-2,0),B(4,0),C(0,3)三点.