题目内容
17.正多边形的一个外角是72°,则这个多边形的内角和的度数是540°.分析 根据任何多边形的外角和都是360°,利用360除以外角的度数就可以求出外角和中外角的个数,即多边形的边数.n边形的内角和是(n-2)•180°,把多边形的边数代入公式,就得到多边形的内角和.
解答 解:多边形的边数:360°÷72°=5,
正多边形的内角和的度数是:(5-2)•180°=540°.
故答案为:540°.
点评 考查了多边形内角与外角,根据外角和的大小与多边形的边数无关,由外角和求正多边形的边数,是常见的题目,需要熟练掌握.

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案
相关题目
5.在一个不透明的袋子中装有仅颜色不同的10个小球,其中红球4个,黑球6个.
(1)先从袋子中取出m(m>1)个红球,再从袋子中随机摸出1个球,将“摸出黑球”记为事件A,请完成下列表格:
(2)先从袋子中取出m个红球,再放入m个一样的黑球并摇匀,随机摸出1个黑球的概率等于$\frac{4}{5}$,求m的值.
(1)先从袋子中取出m(m>1)个红球,再从袋子中随机摸出1个球,将“摸出黑球”记为事件A,请完成下列表格:
| 事件A | 必然事件 | 随机事件 |
| m的值 | 4 | 2,3 |
12. 如图,BD是菱形ABCD的对角线,CE⊥AB交于点E,交BD于点F,且点E是AB中点,则tan∠BFE的值是( )
如图,BD是菱形ABCD的对角线,CE⊥AB交于点E,交BD于点F,且点E是AB中点,则tan∠BFE的值是( )
 如图,BD是菱形ABCD的对角线,CE⊥AB交于点E,交BD于点F,且点E是AB中点,则tan∠BFE的值是( )
如图,BD是菱形ABCD的对角线,CE⊥AB交于点E,交BD于点F,且点E是AB中点,则tan∠BFE的值是( )| A. | $\frac{1}{2}$ | B. | 2 | C. | $\frac{\sqrt{3}}{3}$ | D. | $\sqrt{3}$ |
12.不改变分式的值,将$\frac{x}{2-x}$变形,可得( )
| A. | -$\frac{x}{x+2}$ | B. | $\frac{x}{x-2}$ | C. | -$\frac{x}{x-2}$ | D. | $\frac{x}{x+2}$ |
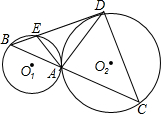 如图,已知⊙O1、⊙O2外切于点A,过点A的直线交⊙O1于B,交⊙O2于C,过点B作直线BD与⊙O1⊙O2分别相交于E,D,连接AE,AD,DC,若AE:AD=ED:DC.
如图,已知⊙O1、⊙O2外切于点A,过点A的直线交⊙O1于B,交⊙O2于C,过点B作直线BD与⊙O1⊙O2分别相交于E,D,连接AE,AD,DC,若AE:AD=ED:DC.