题目内容
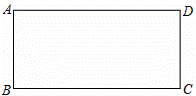
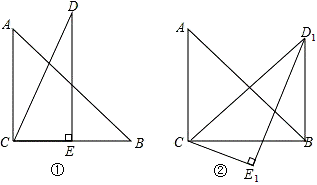
如图，在四边形ABCD中，AB=AD，AC与BD交于点E，∠ADB=∠ACB．
（1）求证：
=
；
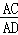（2）若AB⊥AC，AE：EC=1：2，F是BC中点，求证：四边形ABFD是菱形．
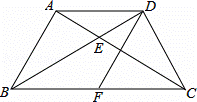
证明：（1）∵AB=AD，∴∠ADB=∠ABE，又∵∠ADB=∠ACB，∴∠ABE=∠ACB，
又∵∠BAE=∠CAB，∴△ABE∽△ACB，∴=
，又∵AB=AD，∴
=
；
（2）设AE=x，∵AE：EC=1：2，∴EC=2x，
由（1）得：AB2=AE•AC，∴AB=
x，又∵BA⊥AC，∴BC=2x，∴∠ACB=30°，
∵F是BC中点，∴BF=x，∴BF=AB=AD，
又∵∠ADB=∠ACB=∠ABD，∴∠ADB=∠CBD=30°，∴AD∥BF，
∴四边形ABFD是平行四边形，又∵AD=AB，∴四边形ABFD是菱形．
练习册系列答案
名题金卷系列答案
相关题目
。
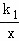（x＞0）的图象经过线段OC的中点A，交DC于点E，交BC于点F．设直线EF的解析式为y=k2x+b．
的相反数是…………………………………………………………………………（ ）
D．
