题目内容
17.已知x=$\sqrt{3}$+$\sqrt{2}$,y=$\sqrt{3}-\sqrt{2}$,求3x2-2xy+3y2的值.分析 把3x2-2xy+3y2化为3(x-y)2+4xy,把x=$\sqrt{3}$+$\sqrt{2}$,y=$\sqrt{3}-\sqrt{2}$代入求解即可.
解答 解:∵x=$\sqrt{3}$+$\sqrt{2}$,y=$\sqrt{3}-\sqrt{2}$,
∴3x2-2xy+3y2
=3(x-y)2+4xy
=3[$\sqrt{3}$+$\sqrt{2}$-($\sqrt{3}-\sqrt{2}$)]2+4×($\sqrt{3}$+$\sqrt{2}$)($\sqrt{3}-\sqrt{2}$)
=8+4
=12.
点评 本题主要考查了二次根式的化简求值,解题的关键是正确的化简来简化运算.

练习册系列答案
相关题目
17.下列事件发生的概率为0的是( )
| A. | 射击运动员只射击1次,就命中靶心 | |
| B. | 任取一个实数x,都有|x|≥0 | |
| C. | 画一个三角形,使其三边的长分别为8cm,6cm,2cm | |
| D. | 抛掷一枚质地均匀且六个面分别刻有1到6的点数的正方体骰子,朝上一面的点数为6 |
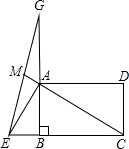 如图,矩形ABCD中,AB=3,AD=3$\sqrt{3}$,点E在CB的延长线上,且BE=$\sqrt{3}$,连结AE,G是BA延长线上一点,连结EG,交CA的延长线于M,将△AEG绕点A逆时针旋转60°得到△AE′G′(点E的对应点为E′,点G的对应点为G′).若△EGG′的面积为6$\sqrt{3}$,则CM的长为7.
如图,矩形ABCD中,AB=3,AD=3$\sqrt{3}$,点E在CB的延长线上,且BE=$\sqrt{3}$,连结AE,G是BA延长线上一点,连结EG,交CA的延长线于M,将△AEG绕点A逆时针旋转60°得到△AE′G′(点E的对应点为E′,点G的对应点为G′).若△EGG′的面积为6$\sqrt{3}$,则CM的长为7. 如图,已知直线a,b,c两两相交,∠1=2∠3,∠2=84°,求∠4的度数.
如图,已知直线a,b,c两两相交,∠1=2∠3,∠2=84°,求∠4的度数.